Cách tìm n để biểu thức có giá trị nguyên cực hay
Cách tìm n để biểu thức có giá trị nguyên cực hay
Tài liệu Cách tìm n để biểu thức có giá trị nguyên cực hay Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.
A. Phương pháp giải
Để biểu thức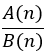 
có giá trị nguyên ta làm như sau:
+ Chia đa thức A(n) cho đa thức B(n) – khi bậc của đa thức A(n) lớn hơn hoặc bằng bậc của đa thức B(n)
+ Biến đổi: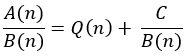 
Để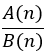
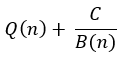
nguyên khi 
nguyên
Suy ra: CMB(n); B(n) ∈ U(C)
Tìm các ước của C. Suy ra, các trường hợp của B(n)
Từ đó, suy ra các giá trị nguyên của n thỏa mãn.
B. Ví dụ minh họa
Ví dụ 1. Tìm n nguyên để ( n + 1) chia hết cho ( n – 1)
A. n ∈ {0; 2; 3; -1} B. n ∈ {1; 2; 4; -1} C. n ∈ {4; 2; 3; 1} D. Đáp án khác
Lời giải
Ta có: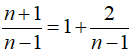 
Do đó, để (n + 1) chia hết cho ( n – 1) thì Ư(2)
Mà Ư(2) = {-1; 1; 2; -2}
+ Nếu n – 1 = -1 thì n =0
+ Nếu n – 1= 1 thì n = 2
+ Nếu n - 1 = 2 thì n = 3.
+ Nếu n – 1 = -2 thì n = -1
Vậy để (n + 1) chia hết cho ( n – 1) thì n ∈ {0; 2; 3; -1}
Chọn A.
Ví dụ 2. Có bao nhiêu giá trị nguyên của n để n2 chia hết cho (n + 2)
A.4 B. 5 C. 6 D. 7
Lời giải
Ta có: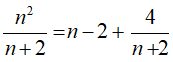 
Để n2 chia hết cho (n + 2) thì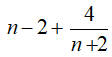 
nguyên
Suy ra,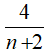 
nguyên nên (n+ 2)∈ Ư (4)
Mà Ư(4) = {-1; 1; -2; 2; -4; 4}
Vậy để n2 chia hết cho (n + 2) thì n ∈ {-3; -1; -4; 0; -6; 2}
Vậy có 6 giá trị nguyên của n thỏa mãn .
Chọn C.
Ví dụ 3. Có bao nhiêu số nguyên dương n thỏa mãn n3 - 28 chia hết cho n- 3
A. 1 B. 2 C. 3 D. 4
Lời giải
Ta có: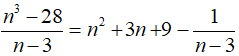 
Để n3 - 28 chia hết cho n- 3 khi và chỉ khi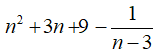 
nguyên
Suy ra: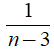 
nguyên.
Do đó, (n – 3) ∈ U(3) = {-1; 1}
+ Nếu n – 3 = -1 thì n = 2
+ Nếu n – 3 = 1 thì n = 4
Vậy có 2 giá trị nguyên dương của n thỏa mãn.
Chọn B.
Ví dụ 4. Có bao nhiêu giá trị nguyên của n để ( 6n+ 5) chia hết cho (3n + 1)
A. 1 B. 2 C. 3 D .4
Lời giải
Ta có: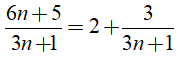 
Để ( 6n +5) chia hết cho (3n + 1) thì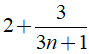 
nguyên
Suy ra: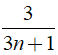
nguyên nên (3n + 1) ∈ U(3) = {-3; -1; 1; 3}
Vậy chỉ có đúng 1 giá trị nguyên của n thỏa mãn là n = 0
Chọn A
C. Bài tập trắc nghiệm
Câu 1: Có bao nhiêu số nguyên n thỏa mãn n3 + 6n2 - 7n + 4 chia hết cho n – 2 ?
A. 6 B. 5 C. 7 D. 8
Ta có
n3 + 6n2 - 7n + 4 = (n3 - 3n2.2 + 3.n.22 - 8) + 12n2 - 19n + 12
= (n - 2)3 + 12n(n - 2) + 5(n - 2) + 22
Khi đó ta có: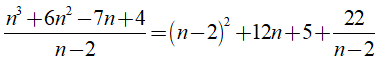 
Để giá trị của biểu thức n3 + 6n2 - 7n + 4 chia hết cho giá trị của biểu thức n - 2
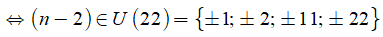
=> n ∈ {1; 3; 0; 4; 13; -9; 24; -20}
Vậy có 8 giá trị nguyên của n thỏa mãn.
Chọn D.
Câu 2. Có bao nhiêu giá trị nguyên dương của n để -2n2 - 4 chia hết cho n + 1
A. 1 B. 2 C. 3 D. 4
Ta có: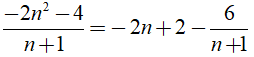 
Để -2n2 - 4 chia hết cho n + 1 thì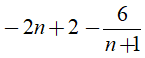 
nguyên
Suy ra: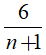 
nguyên. Do đó, (n +1) ∈ U(6) = {-6; -3; -2; -1; 1; 2; 3; 6}
Mà n nguyên dương nên n ∈ {1; 2; 5}
Vậy có 3 giá trị nguyên dương thỏa mãn đầu bài
Chọn C.
Câu 3. Tìm các giá trị nguyên của n để (-3n3 + 2n2 - 31) chia hết cho n + 2
A. -3 và 4 B. -2 và - 4 C. – 1 và 3 D. – 3 và - 1
Ta có: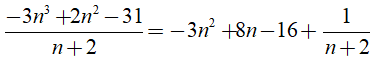 
Để (-3n3 + 2n2 - 31) chia hết cho n + 2 khi và chỉ khi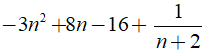 
nguyên
Suy ra: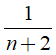
nguyên nên (n + 2)∈ U(1) = {-1; 1}
+ Nếu n + 2 = -1 thì n = -3
+ Nếu n + 2 = 1 thì n = -1
Vậy có 2 giá trị nguyên của n thỏa mãn là – 3 và -1
Chọn D.
Câu 4. Tìm các giá trị nguyên dương của n để (4n2 + 1) chia hết cho n + 2
A. 13 và 15 B. 15 C. 13 và 17 D. 13 và 11
Ta có: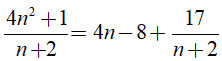 
Để (4n2 + 1) chia hết cho n + 2 thì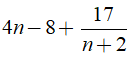 
nguyên
Suy ra: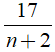
nguyên nên (n +2)∈ U(17) = {-17; -1; 1; 17}
Vậy chỉ có đúng 1 giá trị nguyên dương của n thỏa mãn là n = 15.
Chọn B.
Câu 5. Tìm các giá trị nguyên âm của n để -2n2 + 8n + 43 chia hết cho ( n +3)
A. -4 và – 2 B. -4 và - 1 C. -2 và - 1 D. 2 và - 1
Ta có: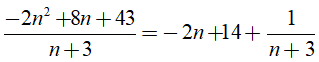 
Để -2n2 + 8n + 43 chia hết cho ( n +3 ) thì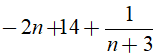 
nguyên
Suy ra: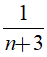 
nguyên nên ( n +3) .
+ Nếu n + 3 = -1 thì n = - 4
+ Nếu n + 3 = 1 thì n = - 2
Vậy có 2 giá trị nguyên âm của n thỏa mãn là – 4 và – 2
Chọn A
Câu 6. Có bao nhiêu giá trị nguyên của n thỏa mãn n3 + 2 chia hết cho n – 3
A.2 B. 3 C. 4 D. 5
Ta có: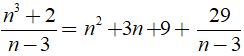 
Để n3 + 2 chia hết cho n – 3 thì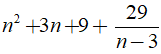 
nguyên
Suy ra: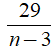
nguyên nên (n – 3) ∈ U(29) = {-29; -1; 1; 29}
Vậy có 4 giá trị nguyên của n thỏa mãn
Chọn C
Câu 7. Có bao nhiêu giá trị nguyên của n thỏa mãn n4 + 2n2 + 1 chia hết cho (n + 2)
A. 5 B. 6 C. 7 D. 8
Ta có: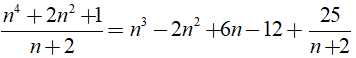 
Để nn4 + 2n2 + 1 chia hết cho (n + 2) thì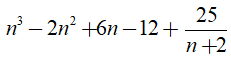 
nguyên
Suy ra: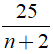
nguyên nên (n +2) ∈ U(25) = {-25; -5; -1; 1; 5; 25}
Vậy có 6 giá trị nguyên của n thỏa mãn
Chọn B
Câu 8. Có bao nhiêu số nguyên n thỏa mãn 4n + 2 chia hết cho 2n – 1
A.1 B. 2 C. 4 D. 6
Ta có: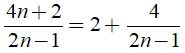 
Để ( 4n +2) chia hết cho 2n – 1 thì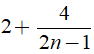 
nguyên
Suy ra: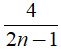 
nguyên nên ( 2n – 1)∈ U(4) = {-1; -2; -4; 1; 2; 4}
Vậy có 2 giá trị nguyên của n thỏa mãn là 0 và 1
Chọn B.
