Các dạng toán về đối xứng trục, đối xứng tâm và cách giải
Các dạng toán về đối xứng trục, đối xứng tâm và cách giải
Tài liệu Các dạng toán về đối xứng trục, đối xứng tâm và cách giải Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

I. Lý thuyết
1. Đối xứng trục
a) Định nghĩa đối xứng trục
+ Hai điểm được gọi là đối xứng với nhau qua một đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó.
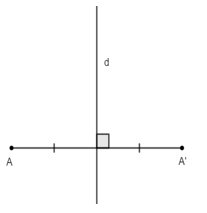
A đối xứng với A’ qua d khi d là trung trực của đoạn thẳng AA’
d ⊥ AA'
+ Quy ước: Một điểm nằm trên trục đối xứng thì điểm đối xứng với nó là chính nó.
+ Điểm nằm trên trục đối xứng thì cách đều hai đầu đoạn thẳng.
b) Hai hình đối xứng qua một trục
Hai hình đối xứng với nhau qua một đường thẳng là luôn có một điểm bất kỳ của hình này đối xứng với một điểm của hình kia qua đường thẳng và ngược lại.
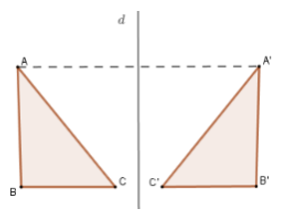
+ Nếu hai đoạn thẳng, góc, tam giác đối xứng với nhau qua một đường thẳng thì bằng nhau.
c) Hình có trục đối xứng
Hình có trục đối xứng: Đường thẳng d được gọi là trục đối xứng của hình 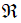 nếu mỗi điểm đối xứng với mỗi điểm thuộc hình qua đường thẳng d cũng thuộc hình
nếu mỗi điểm đối xứng với mỗi điểm thuộc hình qua đường thẳng d cũng thuộc hình 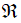 .
.
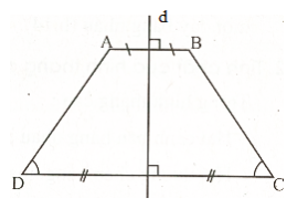
+ Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
2. Đối xứng tâm
a) Định nghĩa
Hai điểm được gọi là đối xứng với nhau qua một điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.
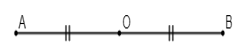
A đối xứng với B qua O
⇔ O là trung điểm của AB
Quy ước: Điểm đối xứng với điểm O chính là điểm O.
b) Hai hình đối xứng nhau qua một điểm
Hai hình gọi là đối xứng với nhau qua một điểm O nếu bất kỳ một điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua O và ngược lại.
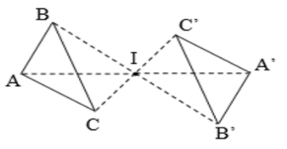
Tam giác ABC và tam giác A’B’C’ đối xứng với nhau qua tâm I
Nhận xét: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một điểm thì bằng nhau.
c) Hình có tâm đối xứng
Điểm O gọi là tâm đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H cũng thuộc hình H.
Hình bình hành có tâm đối xứng là giao điểm của hai đường chéo.
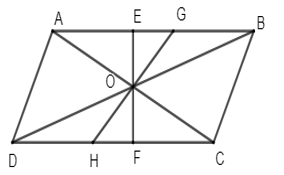
Hình bình hành ABCD có O là giao điểm hai đường chéo nên O là tâm đối xứng của hình bình hành.

II. Các dạng bài tập
Dạng 1. Chứng minh hai điểm hoặc hai hình đối xứng với nhau qua một trục hoặc một tâm
Phương pháp giải: Sử dụng định nghĩa về hai điểm, hai hình đối xứng với nhau qua một trục hoặc một tâm
Ví dụ 1: Cho tam giác ABC cân tại A, AM là đường trung tuyến. Chứng minh AB và AC đối xứng với nhau qua AM.
Lời giải:
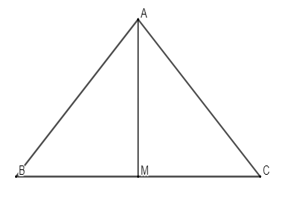
Vì ABC là tam giác cân tại A nên AM vừa là đường trung tuyến vừa là đường cao
=> AM ⊥ BC
AM là trung tuyến nên M là trung điểm của BC, suy ra BM = MC mà AM ⊥ BC nên B đối xứng với C qua AM.
Mặt khác: A ∈ AM nên A đối xứng với A qua AM.
=> AB đối xứng với AC qua AM
Ví dụ 2: Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh AD, BC ở E và F. Chứng minh E và F đối xứng với nhau qua O.
Lời giải:
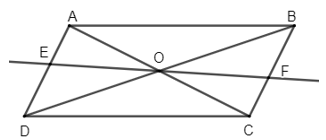
Vì ABCD là hình bình hành
=> AD // BC
=> 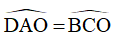 (hai góc so le trong)
(hai góc so le trong)
Có O là giao điểm của hai đường chéo AC và BD
=> O là trung điểm của AC
=> AO = OC
Xét tam giác AOE và tam giác COF có:
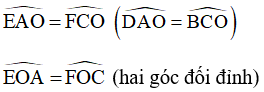
AO = OC
Do đó: ΔAOE = ΔCOF (g – c – g)
=> OE = OF (hai cạnh tương ứng)
Mà O, E, F thẳng hàng nên E đối xứng với F qua O
Dạng 2. Sử dụng tính chất đối xứng trục đối xứng tâm để giải toán
Phương pháp giải: Sử dụng nhận xét hai đoạn thẳng, hai tam giác, hai hình đối xứng với nhau qua trục hoặc tâm thì bằng nhau
Ví dụ 1: Cho tam giác ABC vuông tại A. Lấy M bất kỳ trên cạnh BC. Gọi E và F là điểm đối xứng của M qua AB và AC. Chứng minh A là trung điểm của EF.
Lời giải:
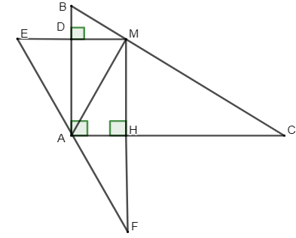
Gọi D là giao điểm của ME và AB, H là giao điểm của MF và AC.
Vì E đối xứng với M qua AB nên ED = MD; 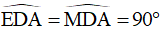
Xét tam giác EDA và tam giác MDA có
DA chung
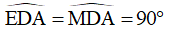
ED = MD
Do đó: ΔEDA = ΔMDA (c – g – c)
=> EA = AM (hai cạnh tương ứng) (1); 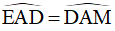 (hai góc tương ứng) (2)
(hai góc tương ứng) (2)
Vì F đối xứng với M qua AC nên FH = MH; 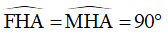
Xét tam giác FHA và tam giác MHA có
HA chung
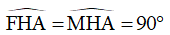
FH = MH
Do đó: ΔFHA = ΔMHA (c – g – c)
=> FA = AM (hai cạnh tương ứng) (3); 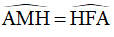 (hai góc tương ứng) (4)
(hai góc tương ứng) (4)
Từ (1) và (3) => EA = FA (5)
Lại có: 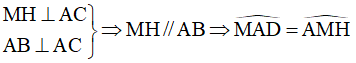 (hai góc so le trong) (6)
(hai góc so le trong) (6)
Từ (2); (4) và (6) => 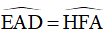
Mà 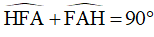 (tam giác AHF vuông tại H)
(tam giác AHF vuông tại H)
Do đó: 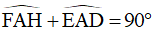
Ta có:
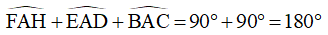
Suy ra A, E, F thẳng hàng (7)
Từ (5) và (7) ta có A là trung điểm của EF.
III. Bài tập tự luyện
Bài 1: Cho tam giác ABC có AB < AC, gọi d là đường trung trực của BC. Vẽ K đối xứng với A qua d.
a) Tìm đoạn thẳng đối xứng với đoạn thẳng AB qua đường thẳng d; tìm đoạn thẳng đối xứng với đoạn thẳng AC qua d;
b) Tứ giác AKCB là hình gì?
Bài 2: Cho tam giác ABC có 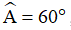 , trực tâm H. Gọi M là điểm đối xứng với H qua BC.
, trực tâm H. Gọi M là điểm đối xứng với H qua BC.
a) Chứng minh ΔBHC = ΔBMC;
b) Tính 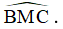
Bài 3: Cho tam giác ABC. Gọi E, F theo thứ tự là trung điểm của các cạnh AB và AC. Một điểm M bất kỳ thuộc cạnh BC, điểm đối xứng với M qua E là P, điểm đối xứng với M qua F là Q.
a) Chứng minh A thuộc đường thẳng PQ;
b) BCQP là hình bình hành.
Bài 4: Cho tam giác ABC, điểm D thuộc cạnh BC. Từ D kẻ đường thẳng song song với cạnh AB, cắt cạnh AC tại E và đường thẳng qua D song song với AC cắt AB tại F. Chứng minh hai điểm E và F đối xứng với nhau qua trung điểm I của đoạn thẳng AD.
Bài 5: Cho tam giác ABC điểm M nằm trên đường phân giác ngoài đỉnh C. Chứng minh: AC + CB < AM + MB.
Bài 6: Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh AD, BC ở E và F. Chứng minh E và F đối xứng với nhau qua O.
Bài 7: Cho tam giác ABC nhọn, lấy M bất kỳ trên BC. Gọi E, F lần lượt là điểm đối xứng với M qua AB và AC. Gọi I và K là giao điểm của EF với AB, AC.
a) Chứng minh: MA là phân giác của 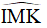
b) Khi M cố định, tìm vị trí điểm P ∈ AB và Q ∈ AC để chu vi tam giác MPQ nhỏ nhất.
Bài 8: Cho góc xOy. Điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy. Tính số đó góc xOy để B đối xứng với C qua O.
Bài 9: Cho tam giác ABC. Vẽ điểm D đối xứng với B qua A, vẽ điểm E đối xứng với C qua A. Gọi M là điểm nằm giữa B và C. Tia MA cắt DE tại N. Chứng minh MC = NE.
Bài 10: Cho hình bình hành ABCD điểm E đối xứng với A qua B, F đối xứng với A qua D. Chứng minh rằng E đối xứng với F qua C.

