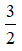Phương pháp Chia đa thức cho một biến đã sắp xếp

Phương pháp Chia đa thức cho một biến đã sắp xếp

Tài liệu Phương pháp Chia đa thức cho một biến đã sắp xếp Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Lý thuyết:

- Muốn chia đa thức một biến A cho đa thức một biến B 0, trước hết ta phải sắp xếp các đa thức này theo lũy thừa giảm dần của cùng một biến và thực hiện phép chia như phép chia các số tự nhiên

- Với A và B là hai đa thức tùy ý cùng một biến số (B ≠ 0), khi đó tồn tại duy nhất một cặp đa thức Q và R sao cho A = B.Q + R.

Trong đó R = 0 hoặc bậc của R nhỏ hơn bậc của B.

Nếu R = 0 thì phép chia A cho B là phép chia hết.

R ≠ 0 thì phép chia A cho B là phép chia có dư.

Q được gọi là đa thức thương, R được gọi là dư trong phép chia A cho B.

B. Các dạng bài:

Dạng 1: Sử dụng hằng đẳng thức để thực hiện phép chia đa thức

1. Phương pháp giải: Có thể dùng các hằng đẳng thức đấng nhớ sau để rút gọn phép chia đa thức:

(A³ + B³) : (A + B) = A² - AB + B²

(A³ - B³) : (A - B) = A² + AB + B²

(A² - B²) : (A + B) = A - B

2. Ví dụ minh hoạ: Áp dụng hẳng đẳng thức đáng nhớ để thực hiện các phép chia sau:

a, (8x³ + 1) : (2x + 1) = [(2x)³ + 1³] : (2x + 1)

= (2x)² - 2x.1 + 1²

= 4x² - 2x + 1

b, (4x² - 4x + 1) : (1 - 2x)

= [(2x)² - 2.2x.1 + 1²] : (1 - 2x)

= (2x - 1)² : (1 - 2x)

= (2x - 1)² : [-(2x - 1)]

= -(2x - 1)

= 1 - 2x

Dạng 2: Tìm thương và số dư trong phép chia đa thức

1. Phương pháp giải: Từ điều kiện đề bài đã cho, đặt phép chia A cho B rồi viết A dưới dạng A = B.Q + R

2. Ví dụ minh họa:

a, Cho hai đa thức A = x³ - x² - 5x - 3 và B = x - 3. Tìm dư R trong phép chia A cho B và viết A dưới dạng A = B.Q + R

b, Cho đa thức A = 3x⁴ + x³ + 6x - 5 và B = x² + 1. Tìm dư R trong phép chia A cho B và viết A dưới dạng A = B.Q + R

Hướng dẫn giải:

a, Ta thực hiện phép chia sau:

(x³ - x² - 5x - 3) : (x - 3)

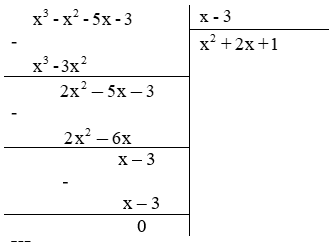
Kết luận:

Vậy số dư trong phép chia là 0

A = (x - 3)(x² + 2x + 1) + 0

b, Ta thực hiện phép chia sau:

(3x⁴ + x³ + 6x - 5) : (x² + 1)

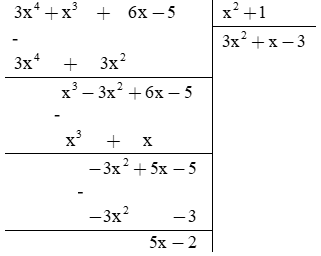
Kết luận:

Vậy số dư trong phép chia là 5x - 2

A = (x² + 1)(3x² + x - 3) + (5x - 2)

Dạng 3: Tìm điều kiện để thực hiện phép chia đa thức

1. Phương pháp giải:

* Thực hiện phép chia A : B để tìm biểu thức dư R theo m

Để A chia hết cho B thì R = 0 => m

* Tìm số nguyên n để A chia hết cho B (với A , B là các biểu thức theo n)

- Thực hiện A : B tìm số dư là số nguyên k, thương là biểu thức Q

- Viết A = Q.B + k

- Để A chia hết cho B ⇔ k chia hết cho B ⇔ B là Ư(k) => n

2. Ví dụ minh họa:

Ví dụ 1: Tìm k để f(x) = x⁴ - 9x³ + 21x² + x + 1 chia hết cho g(x) = x – 2

Lời giải Ta thực hiện phép chia sau:

Để f(x) chia hết cho g(x) thì k + 30 = 0 ⇔ k = - 30.

KL: Vậy với k = -30 thì f(x) chia hết cho g(x)

VD2: Tìm số nguyên x để đa thức A = 8x² - 4x + 1 chia hết cho đa thức B = 2x + 1

Giải: Ta thực hiện phép chia sau:

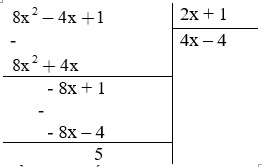
Để A chia hết cho B thì 5 ⋮ (2x + 1) ⇔ (2x + 1) ∈ Ư(5)

KL: Vậy x = {-3, -1, 0, 2}

3, Bài tập tự luyện

Bài 1: Thực hiện phép chia sau:

a, (x³ - x² - 5x - 3) : ( x - 3)

b, ( x⁴ + x³ - 6x² - 5x + 5) : (x² + x - 1)

c, (2x³ + 3x² - 6x + 5) : (x² + 2)

d, (x² + 6x + 7) : (x – 3)

Hướng dẫn giải:

a, Đây là phép chia hết với đa thức thương bằng x² + 2x + 1

b, Đa thức thương bằng x² - 5

c, Đây là phép chia dư với đa thức thương bằng 2x + 3 và dư ( - 10x -1)

d, Đây là phép chia dư với đa thức thương bằng x + 9 và dư 34

Bài 2: Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi tính:

a, (2x⁴ - 5x² + x³ - 3 - 3x) : (x² - 3)

b, (-x³ + 2x⁴ - 4 - x² + 7x) : (x² + x - 1)

c, (-x² + 6x³ - 26x + 21) : (2x – 3)

Hướng dẫn giải:

a, Đây là phép chia hết với đa thức thương bằng 2x² + x + 1

b, Đây là phép chia hết với đa thức thương bằng 2x² - 3x + 4

c, Đây là phép chia hết với đa thức thương bằng 3x² + 4x - 7

Bài 3: Sử dụng hẳng đẳng thức để thực hiện các phép chia sau:

a, (x² + 2x + 1) : (x + 1)

b, (x³ - 8) : (x² + 2x + 4)

c, (x³ - 3x² + 3x - 1) : (x – 1)

d, (8x³ + 27) : (2x + 3)

Hướng dẫn giải:

a, Đa thức thương bằng x + 1

b, x – 2

c, (x – 1)² = x² - 2x + 1

d, 4x² + 6x + 9

Bài 4: Phân tích đa thức thành nhân tử rồi thực hiện phép chia:

a, (24x⁵ - 9x³ + 15x²) : 3x

b, (-8x⁵ + x³ - 2x²) : 2x²

c, (x⁴ + 4x² + 3) : (x² + 3)

d, (x⁴ - 2x³ + 4x² - 4x + 4) : (x² - 2x + 2)

Hướng dẫn giải:

a, 8x⁴ - 3x² + 5x

b,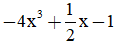

c, x² + 1

d, x² + 2

Bài 5: Tìm thương Q và dư R sao cho A = B.Q + R, biết:

a, A = 2x⁴ + x³ + 3x² + 4x + 9 và B = x² + 1

b, A = 2x³ - 11x² + 19x - 6 và B = x² - 3x + 1

c, A = 2x⁴ - x³ - x² - x + 1 và B = x² + 1

Hướng dẫn giải:

a, Q = 2x² + x + 1 và R = 3x + 8

b, Q = 2x - 5 và R = 2x - 1

c, Q = 2x² - x - 3 và R = 4

Bài 6: Tìm k để:

a, f(x) = x⁴ - 10x³ + 21x² + 8x + k chia hết cho g(x) = x + 2

b, f(x) = x⁴ - 19x³ + 25x² - 6x + k chia hết cho g(x) = x – 3

c, f(x) = x⁴ - 8x³ + 24x² + 7x + k chia hết cho g(x) = x + 4

d, f(x) = 3x⁴ - 7x³ + 11x² + x - k chia hết cho g(x) = x – 4

Hướng dẫn giải:

a, k = - 164

b, k = 225

c, k = -1124

d, k = 500

Bài 7: Tìm a và b để đa thức A chia hết cho đa thức B, biết:

a) A = x⁴ - 3x³ + 3x² + ax + b và B = x² - 3x + 4

b) A = x⁴ - 9x³ + 21x² + ax + b và B = x² - x - 2

Hướng dẫn giải:

a, a = 3, b = -4

b, a = 1, b = -30

Bài 8: Tìm giá trị nguyên của x để đa thức A chia hết cho đa thức B, biết:

a, A = 3x³ + 8x² - 15x + 6 và B = 3x – 1

b, A = x³ + 4x² + 3x - 7 và B = x + 4

Hướng dẫn giải:

a, x = 0, x = 1

b, x = {-23, -5, -3, 15}

Bài 9: Tìm đa thức M, biết:

a) x³ - 5x² + x - 5 = (x - 5).M

b) (x² - 4x - 3).M = 2x⁴ - 13x³ + 14x² + 15x

c) (x² + x + 1).M = x⁴ - x³ - 4x² - 5x - 3

Hướng dẫn giải:

a, M = x² + 1

b, M = 2x² - 5x

c, M = x² - 2x - 3

Bài 10: Tìm x biết:

a) (8x² - 4x) : (-4x) - (x + 2) = 8

b) (2x⁴ - 3x³ + x²) : (-x²) + 4(x - 1)² = 0

Hướng dẫn giải:

a, x = -3

b, x = 1, x =