Cách sử dụng hằng đẳng thức để rút gọn biểu thức cực hay
Cách sử dụng hằng đẳng thức để rút gọn biểu thức cực hay
Tài liệu Cách sử dụng hằng đẳng thức để rút gọn biểu thức cực hay Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải
Haylamdo biên soạn và sưu tầm A, B là các biểu thức tùy ý, ta có:
1.Bình phương của một tổng
(A + B)2 = A2 + 2AB + B2
2.Bình phương của một hiệu
(A - B)2 = A2 - 2AB + B2
3.Hiệu hai bình phương
A2 - B2 = (A - B)(A + B)
4.Lập phương của một tổng
(A + B)3 = A3 + 3A2B + 3AB2 + B3
5.Lập phương của một hiệu.
(A - B)3 = A3 - 3A2B + 3AB2 - B3
6.Tổng hai lập phương
A3 + B3 = (A + B)(A2 - AB + B2)
7.Hiệu hai lập phương
A3 - B3 = (A - B)(A2 + AB + B2)
Chú ý: Ta quy ước A2 + AB + B2 là bình phương thiếu của tổng A + B.
B. Ví dụ minh họa
Ví dụ 1. Tính (a + 3)2
A. a2 + 6a + 9 B. a2 + 3a + 9 C. a2+ 6a + 3 D. a2 +3a + 3
Lời giải
(a + 3)2 = a2 + 2.a.3 + 32 = a2 + 6a + 9
Chọn A.
Ví dụ 2. Viết biểu thức x2 + 4x + 4 dưới dạng bình phương của một tổng.
A. (x+ 4)2 B. (x+2)2 C. (x+ 1)2 D. (2x +1)2
Lời giải
Ta có x2 + 4x + 4 = x2 + 2.x.2 + 22 = (x + 2)2.
Chọn B.
Ví dụ 3. Tính (2x – 3y)2
A. 4x2 - 12xy + y2 B. 4x2 + 12xy - 9y2 C. 4x2 - 6xy + 9y2 D. 4x2 - 12xy + 9y2
Lời giải
Ta có:
(2x - 3y)2 = (2x)2 - 2.2x.3x + (3y)2
= 4x2 - 12xy + 9y2
Chọn D.
Ví dụ 4. Tính (2x – 3y)3
A. 8x3 - 36x2y + 54xy2 - 27y3
B. 8x3 - 36x2y + 27xy2 - 27y3
C. 8x3 - 54x2y + 36xy2 - 27y3
D. 8x3 - 27x2y + 54xy2 - 36y3
Lời giải
Ta có:
(2x - 3y)3 = (2x)3 - 3.(2x)2.3y + 3.2x.(3y)2 - (3y)3
= 8x3 - 36x2y + 54xy2 - 27y3
Chọn A.
C. Bài tập trắc nghiệm
Câu 1. Tính ( 5x -y)2
A. 10x2 - 10xy + y2
B. 25x2 - 5xy + y2
C. 25x2 - 10xy + y2
D. x2 + 10xy + y2
(5x - y)2 = (5x)2 - 2.5x.y + (y)2 = 25x2 - 10xy + y2
Chọn C.
Câu 2. Viết biểu thức 36x2 – 24xy + 4y2 dưới dạng bình phương của một hiệu.
A.( 2x- 2y)2
B. (2x – 6y)2
C. (6x – 6y)2
D. ( 6x- 2y)2
Ta có 36x2 - 24x + 4y2 = (6x)2 - 2.6x.2y + (2y)2 = (6x - 2y)2
Chọn D.
Câu 3. Đưa biểu thức sau về dạng tích 81 – 25x2
A. (3 – 5x). (3+ 5x)
B. (9+ 5x). (9- x)
C. (9+ 5x).(9- 5x)
D. Đáp án khác
Ta có: 81 – 25x2 = 92 – (5x)2 = (9- 5x). ( 9+5x)
Chọn C.
Câu 4 . Tính 56. 64.
A. 3600
B. 2880
C. 3248
D. 3584
Ta có:
56.64 = (60 - 5)(60 + 4) = 602 - 42 = 3600 - 16 = 3584
Chọn D.
Câu 5. Viết biểu thức x3 + 6x2 +12x + 8 dưới dạng lập phương của một tổng.
A. (x+ 1)3
B. (x+ 2)3
C. (2x +1)3
D. (2x +2)3
Ta có: x3 + 6x2 +12x + 8 = x3 + 3.x2.2 + 3.x.22 + 23 = (x+ 2)3
Chọn B.
Câu 6. Khai triển ( 4x – y)3
A. 64x3 - 48x2y + 12xy2 - y3
B. 64x3 - 12x2y + 48xy2 - y3
C. 12x3 - 48x2y + 12xy2 - y3
D. Đáp án khác
(4x - y)3 = (4x)3 - 3.(4x)2.y + 3.4x.y2 - y3
= 64x3 - 48x2y + 12xy2 - y3
Chọn A.
Câu 7. Viết biểu thức x3 - 6x2y + 12xy2 - 8y3 dưới dạng lập phương của một hiệu.
A. (x – 2y)3
B. (2y – x)3
C. ( 2x – 2y)3
D. (x – 4y)3
Ta có :
x3 - 6x2y + 12xy2 - 8y3
= (x)3 - 3.x2.2y + 3x.(2y)2 - (2y)3 = (x - 2y)3
Chọn B.
Câu 8. Viết biểu thức (2x+ 4). (4x2 - 8x +16 ) dưới dạng tổng hai lập phương.
A. 8x3 + 32
B. 8x3 + 12
C. 8x3 + 64
D. 6x3 +12
Ta có: (2x + 4)(4x2 - 8x + 16) = (2x)3 + 43 = 8x3 + 64
Chọn C.
Câu 9. Viết biểu thức (x - 2y)(x2 + 2xy + 4y2) dưới dạng hiệu hai lập phương
A.x3 - 8y3
B. x3 - 6y3
C. 8x3 – y3
D. 2x3 – 4y3
Ta có : (x - 2y)(x2 + 2xy + 4y2) = (x)3 - (2y)3 = x3 - 8y3.
Chọn A.
Câu 10. Viết biểu thức sau dưới dạng hiệu của hai lập phương 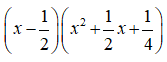
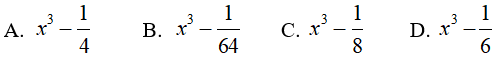
Ta có:

Chọn C.
Câu 11. Tính 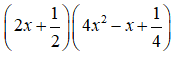
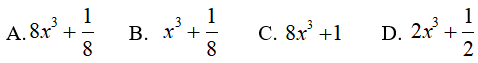
Ta có:
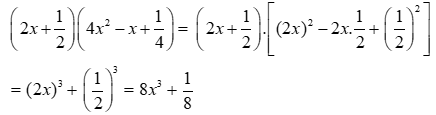
Chọn A.
Câu 12. Tính (3x + 4y). (- 3x + 4y)
A. 9x2 - 16y2
B. -9x2 – 16y2
C. 9x2 + 16y2
D. 16y2 – 9x2
Ta có; (3x + 4y ). (-3x + 4y)= (4y + 3x). ( 4y – 3x)
= (4y)2 - (3x)2 = 16y2 - 9x2
Chọn D.

