Cách vẽ hình đối xứng của một hình cho trước bằng đối xứng tâm

Cách vẽ hình đối xứng của một hình cho trước bằng đối xứng tâm

Tài liệu Cách vẽ hình đối xứng của một hình cho trước bằng đối xứng tâm Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải

Sử dụng định nghĩa, tính chất của phép đối xứng tâm.

a) Hai điểm gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.

Quy ước: Điểm đối xứng với O qua điểm O chính là điểm O.

b) Hai hình gọi là đối xứng với nhau qua điểm O nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua điểm O và ngược lại. Điểm O gọi là tâm đối xứng của hai hình đó.

B. Ví dụ minh họa

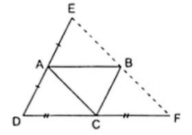
Ví dụ 1. Cho hình bình hình ABCD. Gọi E là điểm đối xứng với D qua điểm A và F là điểm đối xứng với D qua điểm C. Nêu cách vẽ E và F.

Giải

Vẽ các điểm E và F sao cho: A là trung điểm của DE hay DA = AE (1); C là trung điểm của DF hay DC = CF (2) thì E đối xứng với D qua A và F đối xứng với D qua C.

Ví dụ 2. Cho hai điểm A, B nằm cùng phía đối với đường thẳng d. Hình chiếu vuông góc của A, B xuống d lần lượt là H, K. Vẽ hai điểm C đối xứng với A qua H, D đối xứng với B qua K.

Giải

Ta có 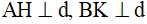. Vẽ hai điểm C, D sao cho H là trung điểm của AC, K là trung điểm của BD ta được C đối xứng với A qua H, D đối xứng với B qua K.

Ví dụ 3. Cho tam giác ABC. Vẽ hình đối xứng với tam giác ABC qua trung điểm của cạnh AC.

Giải

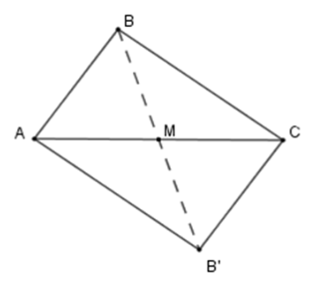
Lấy M là trung điểm AC khi đó A, C đối xứng nhau qua M. Vẽ B’ đối xứng với B qua M bằng cách lấy B’ trên tia đối của tia MB sao cho BM = B’M. Khi đó tam giác CB’A đối xứng với tam giác ABC qua M.