Chứng minh hai đường thẳng vuông góc dựa vào hình chữ nhật

Chứng minh hai đường thẳng vuông góc dựa vào hình chữ nhật

Tài liệu Chứng minh hai đường thẳng vuông góc dựa vào hình chữ nhật Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải

Cách 1:

1. Vẽ thêm hình chữ nhật bằng cách kẻ đường vuông góc hoặc vẽ thêm hình bình hành có một góc vuông.

2. Áp dụng:

• Tính chất về cạnh hoặc đường chéo của hình chữ nhật, định lí Py-ta-go.
• Định lí đường trung tuyến ứng với cạnh huyền của một tam giác vuông bằng một nửa cạnh huyền.

Cách 2:

• Xác định tam giác vuông để vẽ thêm trung tuyến ứng với cạnh huyền.
• Áp dụng tính chất về trung tuyến ứng với cạnh huyền hoặc dấu hiệu nhận biết tam giác vuông.

B. Ví dụ minh họa

Ví dụ 1. Cho hình chữ nhật ABCD. Kẻ BH vuông góc với AC. Gọi M, K lần lượt là trung điểm của AD và HC. Chứng minh rằng BK vuông góc với KM.

Giải

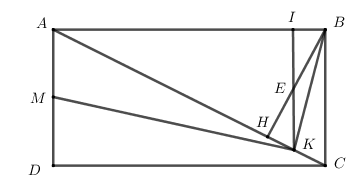
Trong tam giác AKB kẻ đường cao KI cắt BH tại E thì E là trực tâm của tam giác AKB.

Suy ra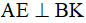

Ta có KI//AD và KI//BC (vì )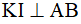

⇒ KE là đường trung bình của tam giác HBC

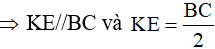
⇒ KE//MA và KE = MA

Do đó tứ giác MAEK là hình bình hành.

Từ đó suy ra AE//MK mà .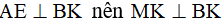

Ví dụ 2. Cho hình thang vuông ABCD có 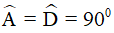và DC = 2AB. Kẻ 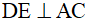gọi I là trung điểm của EC. Chứng minh rằng .

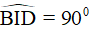Giải

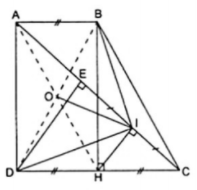
Vẽ 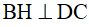thì tứ giác ABHD có ba góc vuông là 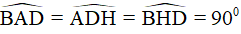nên nó là hình chữ nhật.

Áp dụng tính chất về cạnh và giả thiết vào hình chữ nhật ABHD, ta được:

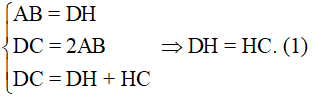
Lại có EI = IC. (2)

Từ (1) và (2) suy ra HI là đường trung bình của tam giác DCE.

Áp dụng định lí đường trung bình vào tam giác DCE thu được HI//DE, do 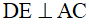theo giả thiết nên 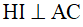hay tam giác AIH vuông tại I.

Áp dụng tính chất về đường chéo vào hình chữ nhật ABHD, gọi O là giao hai đường chéo ta được AO = OH, BO = OD nên IO là trung tuyến của tam giác vuông AIH.

Áp dụng định lí đường trung tuyến ứng với cạnh huyền vào tam giác vuông AHI và tính chất về cạnh vào hình chữ nhật ABHD ta được:

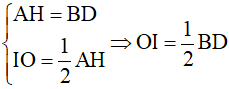
Điều này chứng tỏ trong tam giác BID trung tuyến IO ứng với cạnh BD bằng nửa cạnh ấy nên nó vuông tại I. Vậy .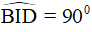

Ví dụ 3. Cho tam giác ABC (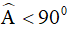). Về phía ngoài của tam giác ABC dựng các hình vuông ABDE, ACFG. Gọi M là trung điểm của đoạn thẳng DF. Chọn câu đúng?

A. Tam giác MBC vuông cân tại M.

B. Tam giác MBC cân tại B.

C. Tam giác MBC cân tại C.

D. Tam giác MBC đều.

Giải

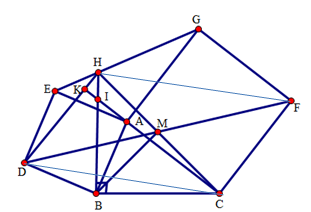
Trên nửa mặt phẳng bờ BC có chứa A dựng tam giác BHC vuông cân đỉnh B.

Xét tam giác BHD và tam giác BCA có:

DB = BA (vì ABDE là hình vuông)

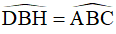(vì cùng phụ với góc HBA)

BH = BC (vì tam giác BHC vuông cân đỉnh B)

Do đó: 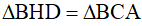(c-g-c), suy ra DH = AC,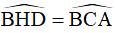

AC cắt HD tại K, cắt BH tại I.

Xét tam giác IHK và tam giác ICB có: 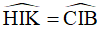(đối đỉnh), 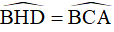(cmt)

do đó 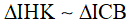suy ra

Mặt khác 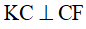, do đó DH//CF.

Ta có DH = CF (= AC) và DH//CF nên DHFC là hình bình hành.

Mà M là trung điểm của DF nên M là trung điểm của HC, suy ra BM là đường trung tuyến của tam giác HBC cân tại H nên BM là đườn cao của tam giác HBC nên BM = MC và .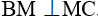

Vậy tam giác MBC vuông cân tại đỉnh M.

Đáp án: A.