Chứng minh hai tam giác đồng dạng - trường hợp đồng dạng thứ ba (G-G)

Chứng minh hai tam giác đồng dạng - trường hợp đồng dạng thứ ba (G-G)

Tài liệu Chứng minh hai tam giác đồng dạng - trường hợp đồng dạng thứ ba (G-G) Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

Dạng bài: Chứng minh hai tam giác đồng dạng theo trường hợp đồng dạng thứ ba

(g – g)

A. Phương pháp giải

Định lí: Nếu hai góc của tam giác này bằng hai góc của tam giác kia thì hai tam giác đồng dạng.

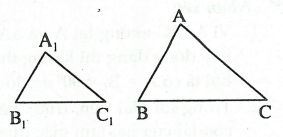Như vậy, nếu hai tam giác ΔABC và ΔA₁B₁C₁ thỏa mãn:

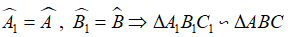
Và khi đó ta có:

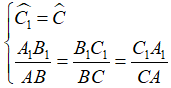
B. Ví dụ minh họa

Câu 1: Tìm trong hình 41 các cặp tam giác đồng dạng.

Lời giải:.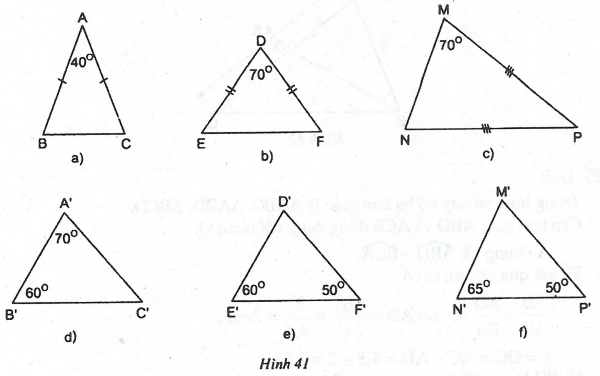

Ta có:

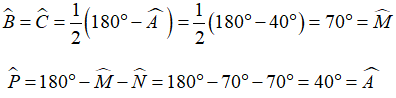
Xét tam giác ABC và PMN có:

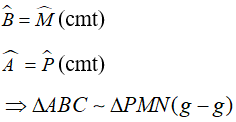
Ta lại có:

Xét Hai tam giác A'B'C' và D'E'F' có:

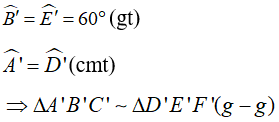
Câu 2: Cho ΔABC, O là điểm ở bên trong tam giác. Kẻ qua O đường thẳng song song với AB cắt AC,BC theo thứ tự tại M,N. Kẻ qua O đường thẳng song song với AC cắt AB,BC theo thứ tự tại P,Q. Hãy vẽ hình và chỉ ra trên hình đó những tam giác đồng dạng và giải thích vì sao chúng đồng dạng?

Lời giải:

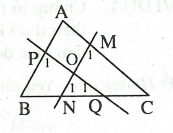
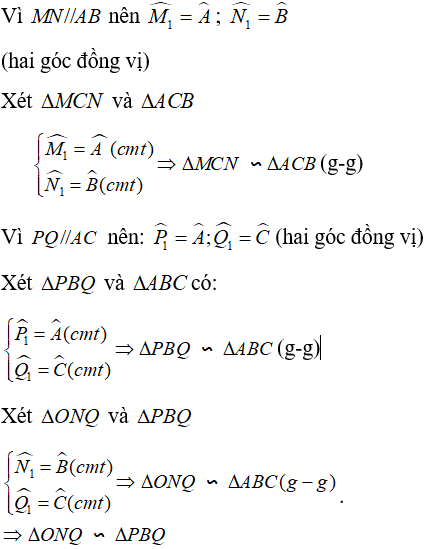
Vậy, ta có được bốn cặp tam giác đồng dạng.

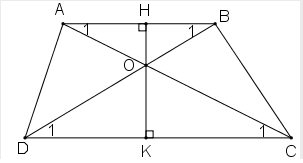
Câu 3: Cho hình thang ABCD (AB//CD). Gọi O là giao điểm của hai đường chéo AC và BD.

a. Chứng minh rằng OA.OD=OB.OC.

b. Đường thẳng qua O vuông góc với AB và CD theo thứ tự tại H và K. Chứng minh rằng .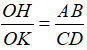

Lời giải:

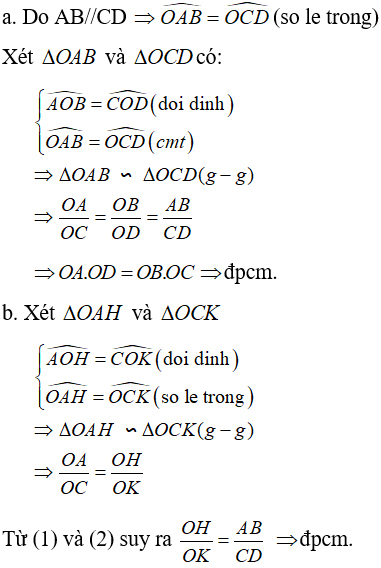
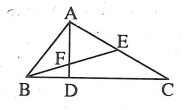
Câu 4: Cho ΔABC vuông tại A, đường cao AD, đường phân giác BE. Giả sử AD cắt BE tại F. Chứng minh rằng .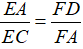

Lời giải:

Trong ΔABD có BF là phân giác suy ra:

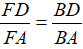(tính chất) (1)

Haylamdo biên soạn và sưu tầm hai tam giác ΔABD và ΔABC, ta có nhận xét:

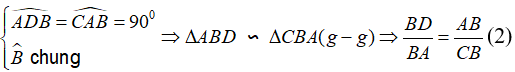
(cặp cạnh tương ứng)

Trong ΔABC có BE là phân giác suy ra:

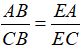(3)

Từ (1), (2), (3) suy ra 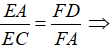đpcm.

C. Bài tập tự luyện

Câu 1: Cho ΔABC có các cạnh AB = 24cm, AC = 28cm. Tia phân giác của góc A cắt cạnh BC tại D. Gọi M,N theo thứ tự là hình chiếu của B và C trên đường thẳng AD.

a. Tính tỉ số .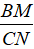

b. Chứng minh rằng .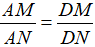

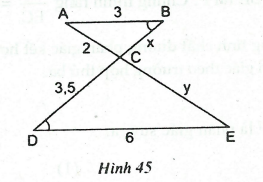
Câu 2: Tính độ dài x,y của các đoạn thẳng trong hình 45.

Câu 3: Cho M là trung điểm cạnh BC của tam giác ABC, biết .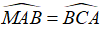

1) Chứng minh rằng hai tam giác ABM và CBA đồng dạng.

2) Chứng tỏ 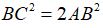. So sánh độ dài cạnh BC với độ dài đường chéo hình vuông có cạnh AB.

3) Phân giác của góc BAC cắt cạnh BC tại I, phân giác của góc AMB cắt cạnh AB tại J. Chứng minh IJ song song với AC.

Câu 4: Cho tam giác ABC vuông tại B với AB=2BC. Lấy điểm D thuộc cạnh AC sao cho BC=CD, điểm E thuộc cạnh AB sao cho AD=AE. Chứng minh rằng .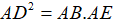

Câu 5: Cho tam giác ABC vuông tại A có AD là đường cao. Đường phân giác góc 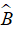lần lượt cắt AD, AC tại F, E. Chứng minh rằng .

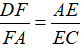Câu 6 : Cho ΔABC có ba góc nhọn, các điểm M và N thứ tự là trung điểm của BC và AC. Gọi H,O,G theo thứ tự là trực tâm, tâm đường tròn ngoại tiếp, trọng tâm của ΔABC.

a. Tìm các tam giác đồng dạng với ΔABH.

b. Chứng minh rằng ΔAHG~ΔOMG.

c. Chứng minh rằng ba điểm H,O,G thẳng hàng.

Câu 7 : Cho ΔABC đều có O là trung điểm cạnh BC. Vẽ góc 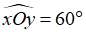sao cho các tia Ox, Oy cắt các cạnh AB, AC lần lượt tại E, F. Chứng minh rằng

Câu 8 : Cho ΔABC vuông tại A, đường cao AH. Gọi M, N lần lượt là trung điểm các đoạn thẳng BH, AH. Chứng minh rằng