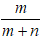Cách chứng minh phân thức là tối giản cực hay, có đáp án
Cách chứng minh phân thức là tối giản cực hay, có đáp án
Tài liệu Cách chứng minh phân thức là tối giản cực hay, có đáp án Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.
A. Phương pháp giải
Gọi ước chung lớn nhất của tử thức và mẫu thức là d, chứng minh d = 1 hoặc d = -1
B. Ví dụ minh họa
Ví dụ 1: Chứng minh phân thức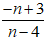 
(với n ∈ N) là tối giản:
Hướng dẫn giải:
Gọi ƯCLN của –n + 3 và n - 4 là d
⇒ (-n + 3)⋮ d và (n - 4)⋮ d
⇒ [(-n + 3) +(n - 4)] ⋮ d
⇒ -1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho là tối giản với ∀n ∈ N
Ví dụ 2: Chứng minh phân thức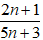 
(với n ∈ N) là tối giản:
Hướng dẫn giải:
Gọi ƯCLN của 2n + 1 và 5n + 3 là d
⇒ (2n +1)⋮ d và (5n + 3)⋮ d
⇒ [2(5n + 3) - 5(2n + 1) ] ⋮ d
⇒ 1 ⋮ d, với ∀n ∈ N
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Ví dụ 3: Chứng minh rằng với mọi số nguyên n thì phân số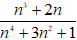 
là phân số tối giản
Hướng dẫn giải:
Gọi d là ƯCLN của n3 + 2n và n4 + 3n2 + 1
Ta có n3 + 2n ⋮ d ⇒ n(n3 + 2n) ⋮ d ⇒ n4 + 2n2 ⋮ d (1)
(n4 + 3n2 + 1) –(n4 + 2n2) ⋮ d
⇒ n2 + 1 ⋮ d⇒ (n2 + 1)2 = n4 + 2n2 + 1 ⋮ d (2)
Từ (1) và (2) suy ra (n4 + 2n2 +1) – (n4 + 2n2) ⋮ d ⇒ 1 ⋮ d ⇒ d = ± 1
Vậy 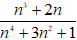là phân số tối giản
C. Bài tập vận dụng
Bài 1: Chứng minh phân thức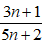 
(với n ∈ N) là tối giản
Hướng dẫn giải:
Gọi ƯCLN của 2n + 1 và 5n + 3 là d
⇒ (3n + 1) ⋮ d và (5n + 2) ⋮ d
⇒ [3(5n + 2) - 5(3n + 1)] ⋮ d
⇒ 1 ⋮ d, với ∀n ∈ N
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Bài 2: Chứng minh phân thức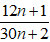 
là tối giản với mọi số tự nhiên n:
Hướng dẫn giải:
Gọi d là ƯCLN của 12n + 1 và 30n + 2
⇒ (12n + 1)⋮ d và (30n + 2)⋮ d
⇒ [5(12n + 1) - 2(30n + 2)] ⋮ d
⇒ 1 ⋮ d, với ∀n ∈ N
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Bài 3: Chứng minh phân thức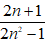 
là tối giản với mọi số tự nhiên n:
Hướng dẫn giải:
Gọi d là ƯCLN của 2n + 1 và 2n2 - 1
⇒ (2n +1)⋮ d và (2n2 -1)⋮ d
⇒ [n(2n + 1) - (2n2 -1)] = n + 1⋮ d
⇒ 2(n + 1) ⋮ d ⇒ (2n + 2) – (2n + 1) = 1 ⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Bài 4: Chứng minh phân thức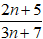 
là tối giản với mọi số tự nhiên n:
Hướng dẫn giải:
Gọi d là ƯCLN của 2n + 5 và 3n + 7
⇒ (2n + 5)⋮ d và (3n + 7)⋮ d
⇒ [3(2n + 5) - 2(3n + 7)] = 1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Bài 5: Chứng minh phân thức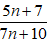 
là tối giản với mọi số tự nhiên n:
Hướng dẫn giải:
Gọi d là ƯCLN của 5n + 7 và 7n + 10
⇒ (5n + 7)⋮ d và (7n + 10)⋮ d
⇒ [7(5n + 7) - 5(7n + 10)] = -1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Bài 6: Chứng minh phân thức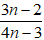 
là tối giản với mọi số tự nhiên n
Hướng dẫn giải:
Gọi d là ƯCLN của 3n - 2 và 4n - 3
⇒ (3n - 2)⋮ d và (4n - 3)⋮ d
⇒ [3(4n - 3) - 4(3n - 2)] = -1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Bài 7: Chứng minh phân thức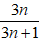 
là tối giản với mọi số tự nhiên n
Hướng dẫn giải:
Gọi d là ƯCLN của 3n và 3n + 1
⇒ 3n ⋮ d và (3n + 1)⋮ d
⇒ [(3n + 1) - 3n ] = 1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Bài 8: Chứng minh phân thức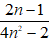 
là tối giản với mọi số tự nhiên n:
Hướng dẫn giải:
Gọi d là ƯCLN của 2n - 1 và 4n2 - 2
⇒ (2n -1)⋮ d và (4n2 - 2)⋮ d
⇒ [2n(2n - 1) - (4n2 - 2)] = -2n + 2⋮ d
⇒ (2n - 1) + (-2n + 2) = 1 ⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Bài 9: Chứng minh phân thức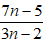 
là tối giản với mọi số tự nhiên n:
Hướng dẫn giải:
Gọi d là ƯCLN của 7n - 5 và 3n - 2
⇒ (7n - 5)⋮ d và (3n - 2)⋮ d
⇒ [3(7n - 5) - 7(3n - 2)] = -1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Bài 10: Cho phân thức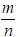 
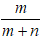
là phân thức tối giản. Chứng minh phân thức 
là phân thức tối giản.
Hướng dẫn giải:
Giả sử m, n là các số nguyên và ƯCLN(m, n) = 1 (vì 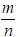tối giản)
nếu d là ước chung m của m + n thì:
(m + n) d và m d
⇒ [(m + n) – m ] = n d
⇒ d ∈ ƯC (m,n) ⇒ d = 1(vì 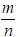tối giản) .
Vậy nếu phân thức là phân thức tối giản thì phân thức cũng là phân thức tối giản.
