Các dạng bài tập Toán 8 Chương 4: Hình lăng trụ đứng. Hình chóp đều chọn lọc
Các dạng bài tập Toán 8 Chương 4: Hình lăng trụ đứng. Hình chóp đều chọn lọc
Haylamdo biên soạn và sưu tầm Các dạng bài tập Chương 4: Hình lăng trụ đứng. Hình chóp đều chọn lọc môn Toán lớp 8 sẽ giúp học sinh nắm vững lý thuyết, biết cách làm các dạng bài tập từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi môn Toán 8.
Mục lục Chương 4: Hình lăng trụ đứng. Hình chóp đều
I/ Lý thuyết & Bài tập theo bài học
- Công thức Hình hộp chữ nhật đầy đủ
- Bài tập Hình hộp chữ nhật
- Lý thuyết Bài 1: Hình hộp chữ nhật
- Lý thuyết Bài 2: Hình hộp chữ nhật (tiếp)
- Lý thuyết Bài 3: Thể tích của hình hộp chữ nhật
- Bài tập Bài 3: Thể tích của hình hộp chữ nhật
- Công thức Hình lăng trụ đứng đầy đủ
- Bài tập Hình lăng trụ đứng
- Lý thuyết Bài 4: Hình lăng trụ đứng
- Lý thuyết Bài 5: Diện tích xung quanh của hình lăng trụ đứng
- Lý thuyết Bài 6: Thể tích của hình lăng trụ đứng
- Lý thuyết Bài 7: Hình chóp đều và hình chóp cụt đều
- Bài tập Bài 7: Hình chóp đều và hình chóp cụt đều
- Công thức Hình chóp đều đầy đủ
- Bài tập Hình chóp đều
- Lý thuyết Bài 8: Diện tích xung quanh của hình chóp đều
- Lý thuyết Bài 9: Thể tích của hình chóp đều
- Tổng hợp Lý thuyết & Trắc nghiệm Chương 4 Hình học 8
II/ Các dạng bài tập
- Vị trí tương đối của hai đường thẳng trong không gian
- Đường thẳng vuông góc với mặt phẳng – Hai mặt phẳng vuông góc
- Tính diện tích xung quanh, diện tích toàn phần, thể tích của hình hộp chữ nhật
- Tìm số mặt, số đỉnh, số cạnh của hình lăng trụ đứng
- Tìm các yếu tố song song, vuông góc trong hình lăng trụ đứng
- Tính diện tích xung quanh, diện tích toàn phần, thể tích của hình lăng trụ đứng
- Tính số mặt, số đỉnh, số cạnh của hình chóp đều
- Chứng minh quan hệ song song, vuông góc, bằng nhau trong hình chóp đều
- Tính diện tích xung quanh, diện tích toàn phần, thể tích của hình chóp đều, hình chóp cụt đều
Dạng bài: Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình hộp chữ nhật
A. Phương pháp giải
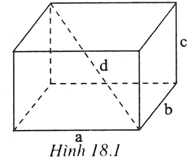
+) Diện tích xung quanh của hình hộp chữ nhật bằng chu vi đáy nhân với chiều cao.
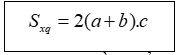
+) Diện tích toàn phần của hình hộp chữ nhật bằng tổng của diện tích xung quanh và diện tích hai đáy.
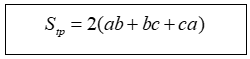
+) Thể tích của hình hộp chữ nhật bằng tích của ba kích thước
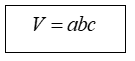
+) Đặc biệt, đối với hình lập phương thì:
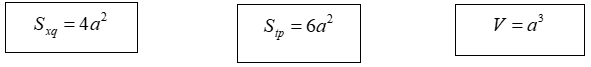
B. Ví dụ minh họa
Câu 1:
a) Tính các kích thước của một hình hộp chữ nhật, biết rằng chúng tỉ lệ với 3, 4, 5 và thể tích của hình hộp này là 480m3.
b) Diện tích toàn phần của một hình lập phương là 486m2. Thể tích của nó là bao nhiêu?
Lời giải:
a) Gọi a, b, c là các kích thước của hình chữ nhật (đơn vị: cm).
Theo đề bài, ta có:
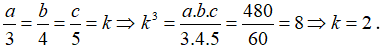
Suy ra a=6; b=8; c=10.
Vậy các kích thước của hình hộp chữ nhật là;
a=6cm; b=8cm; c=10cm.
b) Hình lập phương có 6 mặt là hình vuông bằng nhau.
Gọi a là cạnh của hình vuông (đơn vị: mét).
Ta có, diện tích của hình vuông là: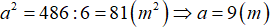 
.
Vậy, thể tích của khối lập phương là: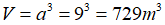 
.
Câu 2: Cho hình hộp chữ nhật có chiều dài bằng 6cm, chiều rộng bằng 1/2 chiều dài và chiều cao gấp 3 lần chiều rộng. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình hộp chữ nhật đó.
Lời giải:
Để tính được diện tích xung quanh, diện tích toàn phần và thể tích của hình chữ nhật, ta cần biết đầy đủ ba kích thước của nó là chiều dài, chiều rộng, chiều cao, từ giả thiết ta có:
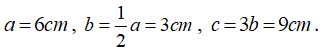
Khi đó:
- Diện tích xung quanh của hình hộp chữ nhật là:
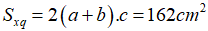
- Diện tích toàn phần của hình hộp chữ nhật là:
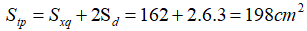
- Thể tích hình hộp chữ nhật là:
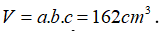
Câu 3: Một bể nước hình chữ nhật có chiều dài 2m. Lúc đầu bể không có nước. Sau khi đổ vào bể 120 thùng nước, mỗi thùng chứa 20 lít thì mực nước của bể cao 0,8m.
a) Tính chiều rộng của bể nước.
b) Người ta đổ thêm vào bể 60 thùng nước nữa thì đầy bể. Hỏi bể cao bao nhiêu mét?
Lời giải:
a) Lượng nước đổ vào bể lúc đầu là: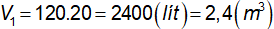 
.
Diện tích đáy của bể là: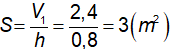 
.
Đáy bể là hình chữ nhật nên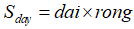 
.
Suy ra, chiều rộng của đáy bể là: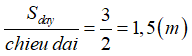 
.
b) Lượng nước đổ vào bể cả hai lần là:
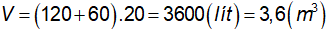
Vậy, chiều cao của bể là: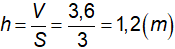 
.
....................................
....................................
....................................
Dạng bài: Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lăng trụ đứng
A. Phương pháp giải
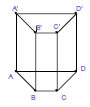
- Các mặt bên là những hình chữ nhật.
- Các cạnh bên song song và bằng nhau.
- Hai đáy là hai đa giác có cạnh tương ứng song song với nhau, hai đáy là hai đa giác bằng nhau.
- Diện tích xung quanh của lăng trụ đứng bằng chu vi đáy nhân với chiều cao:
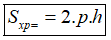
(p là nửa chi vi, h là chiều cao của lăng trụ)
- Thể tích của lăng trụ đứng bằng diện tích đáy nhân với chiều cao:
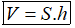
(S diện tích đáy, h chiều cao của lăng trụ đứng)
B. Ví dụ minh họa
Câu 1: Cho hình lăng trụ đứng ABC.A'B'C' đáy là tam giác vuông cân tại A. Biết hình trụ này có chiều cao là 4m và thể tích là 18m3. Tính diện tích toàn phần của nó.
Lời giải:
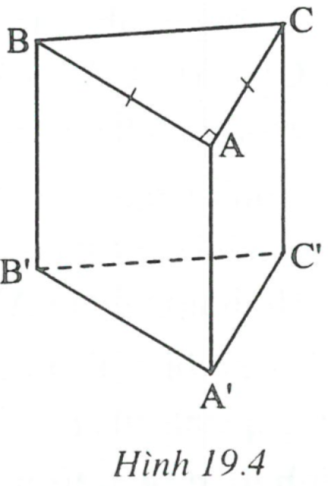Ta có: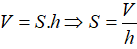 
Vậy diện tích đáy của hình lăng trụ này là:
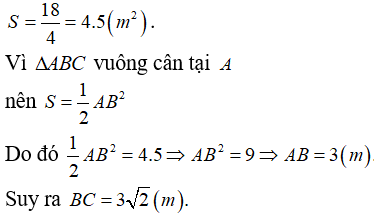
Diện tích xung quanh của hình lăng trụ là:
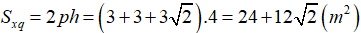
Diện tích toàn phần là: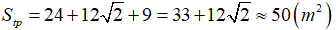 
Câu 2: Tính diện tích xung quanh, diện tích toàn phần của các hình lăng trụ đứng trong hình 102.
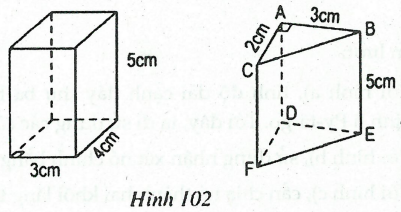
Lời giải:
a) Hình hộp chữ nhật (hình lăng trụ đứng có đáy là hình chữ nhật) có:
- Diện tích xung quanh:
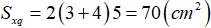
- Diện tích toàn phần:
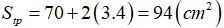
b) Hình lăng trụ đứng tam giác ABC.DEF có ΔABC vuông tại A nên:
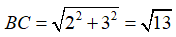
Ta lần lượt có:
- Diện tích xung quanh:
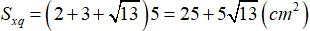
- Diện tích toàn phần:
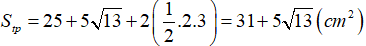
Câu 3: Cho hình lăng trụ đứng ABCD.A1B1C1D1 có đáy ABCD là hình thang vuông (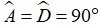
), AB=6cm, CD=2cm, AD=3cm, AA1=5cm. Tính diện tích một đáy, diện tích xung quanh, diện tích toàn phần và thể tích của hình lăng trụ.
Lời giải:
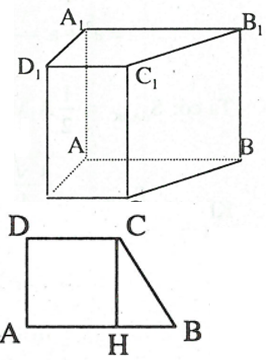Xét hình thang ABCD, hạ CH vuông góc với AB, ta có:
CH=AD=3cm, BH=AB-AH=AB-CD=4cm.
Trong ΔHBC vuông tại H, ta có:
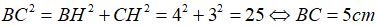
Khi đó, ta lần lượt có:
....................................
....................................
....................................
