Bài tập Những hằng đẳng thức đáng nhớ chọn lọc, có đáp án

Áp dụng hằng đẳng thức (a - b)² = a² - 2ab + b².

Khi đó ta có A = ( 1/2x - y )² = 1/4x² - 2.1/2x.y + y² = 1/4x² - xy + y².

Suy ra chỗ trống cần điền là xy.

Chọn đáp án B.

Áp dụng hằng đẳng thức a³ - b³ = ( a - b )( a² + ab + b² )

Khi đó ta có ( 2x - 1 )( 4x² + 2x + 1 ) = ( 2x - 1 )[ ( 2x )² + 2x.1 + 1 ] = ( 2x )³ - 1 = 8x³ - 1.

Suy ra chỗ trống cần điền là 8x³ - 1.

Chọn đáp án D.

Áp dụng hằng đẳng thức ( a + b )³ = a³ + 3a²b + 3ab² + b³.

Khi đó ta có:

A = 8x³ + 12x²y + 6xy² + y³ = ( 2x )³ + 3.( 2x )².y + 3.( 2x ).y² + y³ = ( 2x + y )³

Haylamdo biên soạn và sưu tầm x = 2 và y = -1 ta có A = ( 2.2 - 1 )³ = 3³ = 27.

Chọn đáp án C.

Ta có A = 35² - 700 + 10² = 35² - 2.35.10 + 10²

Áp dụng hằng đẳng thức ( a - b )² = a² - 2ab + b².

Khi đó A = ( 35 - 10 )² = 25².

Chọn đáp án A.

Ta có 2x² - 4x + 2 = 0 ⇔ 2( x² - 2x + 1 ) = 0        ( 1 )

Áp dụng hằng đẳng thức ( a - b )² = a² - 2ab + b²

Khi đó ta có ( 1 ) ⇔ 2( x - 1 )² = 0 ⇔ x - 1 = 0 ⇔ x = 1.

Chọn đáp án A.

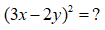
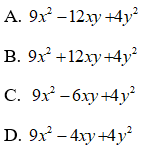
Áp dụng hằng đẳng thức đáng nhớ:

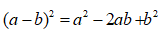
Ta được:

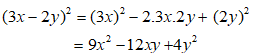
Chọn đáp án A

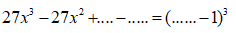
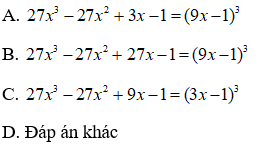
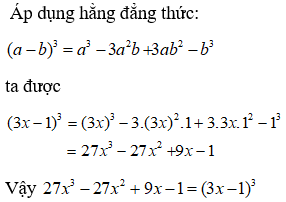
Chọn đáp án C

Áp dụng hằng đẳng thức:

a³ – b³ = (a – b).(a² + ab + b²) và a³ + b³ = (a + b).(a² – ab + b²) ta được:

A = (x – 2y). (x² + 2xy + y²) - (x + 2y). (x² – 2xy + y²)

A = x³ – (2y)³ - [x³ + (2y)³]

A = x³ – 8y³ – x³ – 8y³ = -16y³

Chọn đáp án B

Ta có: x² – 16 + x(x – 4) = 0

⇔ (x + 4). (x - 4) + x.(x – 4) = 0

⇔ (x + 4 + x).(x - 4) = 0

⇔ (2x + 4). (x - 4) = 0

⇔ 2x + 4 = 0 hoặc x – 4 = 0

* Nếu 2x + 4 = 0 thì x = -2

* Nếu x – 4 =0 thì x = 4

Vậy x = -2 hoặc x = 4.

Chọn đáp án D

Ta có: A = (x + 2y ). (x - 2y) - (x – 2y)²

A = x² – (2y)² – [x² – 2.x.2y +(2y)² ]

A = x² – 4y² – x² + 4xy - 4y²2

A = -8y² + 4xy

Chọn đáp án B