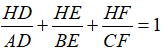Cách chứng minh đẳng thức hình học bằng cách sử dụng diện tích

Cách chứng minh đẳng thức hình học bằng cách sử dụng diện tích

Tài liệu Cách chứng minh đẳng thức hình học bằng cách sử dụng diện tích Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

Dạng bài: Sử dụng diện tích để chứng minh

A. Phương pháp giải

Phát hiện quan hệ giữa các yếu tố trong hình với diện tích rồi sử dụng công thức diện tích.

B. Ví dụ minh họa

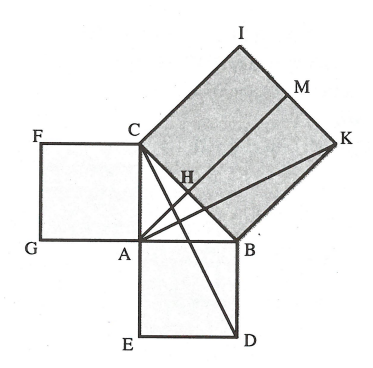
Câu 1: Cho tam giác ABC vuông tại A. Dựng các hình vuông bên ngoài tam giác như hình vẽ. AH là đường cao, AH kéo dài cắt KI tại M.

a) Chứng minh rằng: ΔDBC = ΔABK

b) Suy ra diện tích ΔDBC = diện tích ΔABK

c) Chứng minh rằng:

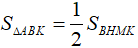
Lời giải:

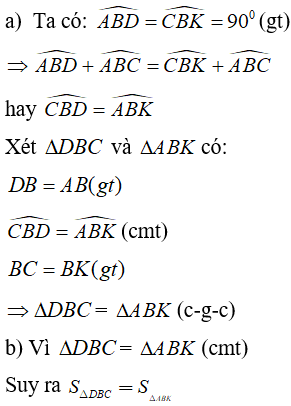
c) Hai tam giác ADB và DBC có cùng chiều cao bằng AB ứng với cạnh đáy chung là DB nên có diện tích bằng nhau. Mặt khác, diện tích tam giác ADB bằng nửa diện tích hình vuông ABDE nên ta có: diện tích ΔDBC= 1/2 diện tích (ABDE).

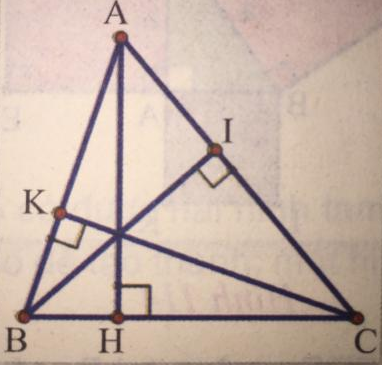
Câu 2: Cho tam giác ABC với các đường cao AH, BI, CK (hình 118).

Chứng minh rằng: AH. BC = BI. CA = CK. AB

Giải.

Giải.

Ta có:

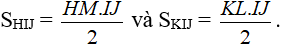
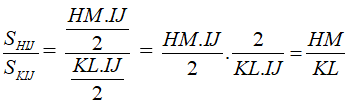
⇒Đpcm

b) Vì AH, BI, CK đều là đường cao của tam giác ABC nên ta có:

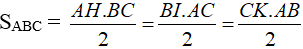
⇒ AH. BC = BI. CA = CK. AB (đpcm).

Câu 3: Cho tam giác đều ABC. Từ điểm O ở trong tam giác ta vẽ 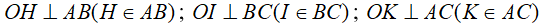. Chứng minh rằng khi O di động trong tam giác thì tổng OH + OI + OK không thay đổi.

Lời giải:

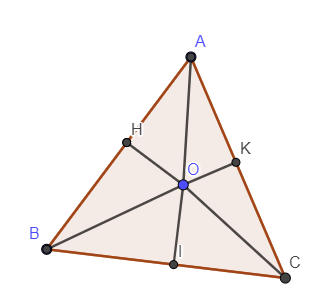
Gọi độ dài mỗi cạnh của tam giác đều là a, chiều cao là h.

Ta có:

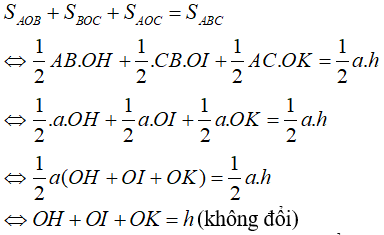
Vậy khi O di động trong tam giác thì tổng OH + OI + OK không thay đổi.

C. Bài tập tự luyện

Câu 1: Cho hình bình hành ABCD. Kẻ AI, CH vuông góc với đường chéo BD. Chứng minh ΔADI và ΔBCH có diện tích bằng nhau.

Câu 2: Cho hình vuông ABCD cạnh a. Trên AB, CD lấy

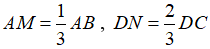
a) Chứng minh ADCM, ABCN có diện tích bằng nhau;

b) Tính diện tích AMCN theo a.

Câu 3: Cho ΔABC, trên tia đối của các tia BA, CB, AC lấy M, N, P sao cho BA = BM, CN = CB, AP = AC. Chứng minh .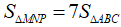

Câu 4: Cho 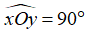có tia Oz là phân giác. Lấy điểm P cố định thuộc Oz (P ≠ O). Qua P kẻ đường thẳng d bất kỳ cắt Ox, Oy lần lượt tại M, N. Chứng minh khi d thay đổi thì 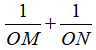không đổi.

Câu 5: Cho ΔABC có độ dài ba đường cao ứng với các cạnh BC, CA, AB là h_a, h_b, h_c. Từ điểm O bất kỳ trong tam giác, vẽ các đoạn thẳng có độ dài x, y, z vuông góc với BC, CA, AB. Chứng minh

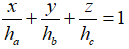
Câu 6: Cho ΔABC có ba đường cao AD, BE, CF cắt nhau tại H. Chứng minh