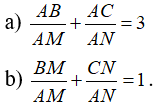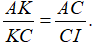Chứng minh các hệ thức bằng định lí Ta-lét trong tam giác

Chứng minh các hệ thức bằng định lí Ta-lét trong tam giác

Tài liệu Chứng minh các hệ thức bằng định lí Ta-lét trong tam giác Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

Dạng bài: Chứng minh các hệ thức bằng định lí Ta-lét trong tam giác

A. Phương pháp giải

+) Vận dụng định lí Ta-lét.

+) Sử dụng tính chất của tỉ lệ thức.

B. Ví dụ minh họa

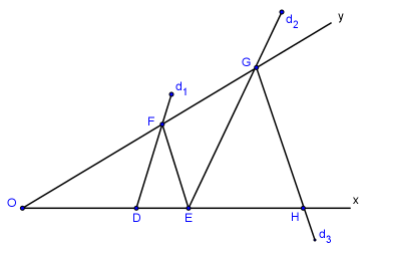
Câu 1: Cho góc nhọn xOy. Trên tia Ox lấy hai điểm D, E. Một đường thẳng d₁ qua D cắt tia Oy tại điểm F, đường thẳng d₂ đi qua E và song song với d₁, cắt tia Oy tại điểm G. Đường thẳng d₃ qua G và song song với EF, cắt tia Ox tại điểm H.

Chứng minh: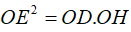

Lời giải:

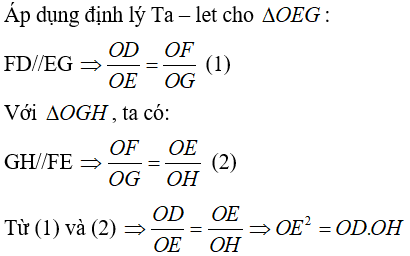
Câu 2: Cho tam giác ABC, M là một điểm bất kì trên BC. Các đường song song với AM vẽ từ B và C cắt AC, AB tại N và P. Chứng minh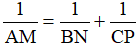

Lời giải:

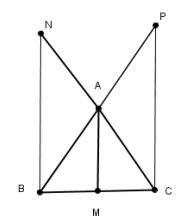Áp dụng định lý Talet cho tam giác BNC (AM//BN) :

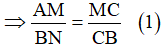
và tam giác CPB (AM//CP):

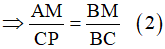
Lấy vế với vế của (1)+(2) ta được

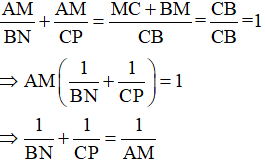
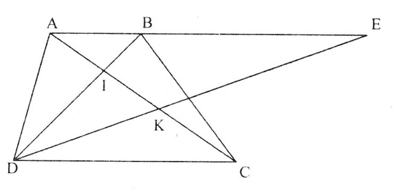
Câu 3: Cho hình thang ABCD (AB // CD, AB < CD). Gọi trung điểm của các đường chéo AC, BD theo thứ tự N và M. Chứng minh rằng:

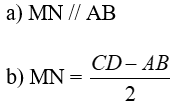
Lời giải:

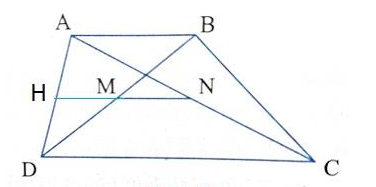
Gọi H là trung điểm AD, N là trung điểm AC ⇒HN là đường trung bình của ΔADC

⇒ HN // DC

Vì H là trung điểm AD, M là trung điểm BD ⇒ HM là đường trung bình trong ΔABD

⇒ HM // AB

Mặt khác AB // CD(gt) ⇒ HM // HN // AB ⇒ H, M, N thẳng hàng và MN // AB.

b) Ta có: HN là đường trung bình trong ΔADC(cmt)

⇒ HN =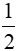 CD

Có: HM là đường trung bình trong ΔABD

⇒ HM = 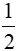AB

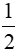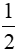Ta có: MN = HN - HM = CD - AB =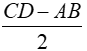

C. Bài tập tự luyện

Câu 1: Cho biết 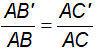. Chứng minh rằng:

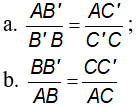
Câu 2: Cho tam giác ABC. Một đường thẳng song song với BC cắt các cạnh AB và AC theo thứ tự ở D và E. Chứng minh rằng: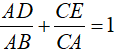

Câu 3: Cho ΔABC. Lấy điểm D thuộc đoạn AB, điểm E thuộc tia đối của tia CA sao cho DB=CE, DE cắt BC tại M. Chứng minh .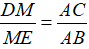

Câu 4: Cho ΔABC có AD là đường trung tuyến, G là trọng tâm. Qua G kẻ đường thẳng d cắt AB, AC thứ tự tại M, N. Chứng minh: