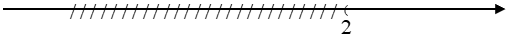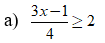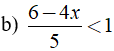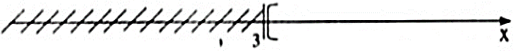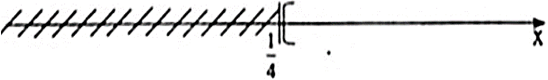Lý thuyết Bất phương trình một ẩn hay, chi tiết

Lý thuyết Bất phương trình một ẩn hay, chi tiết

Haylamdo biên soạn và sưu tầm Lý thuyết Bất phương trình một ẩn hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Lý thuyết

1. Bất phương trình một ẩn

Bất phương trình ẩn x là hệ thức A( x ) > B( x ) hoặc A( x ) < B( x ) hoặc A( x ) ≥ B( x ) hoặc A( x ) ≤ B( x ).

Trong đó: A( x ) gọi là vế trái; B( x ) gọi là vế phải.

Nghiệm của bất phương trình là giá trị của ẩn thay vào bất phương trình ta được một khẳng định đúng.

Ví dụ:

Các phương trình một ẩn như: x - 1 < 2x - 3; (x + 1)/2 > - 3; 2( x - 1 ) ≤ 1 - 3x; 1 - x ≥ 2; ...

2. Tập nghiệm của bất phương trình

Tập hợp tất cả các nghiệm của bất phương trình được gọi là tập nghiệm của bất phương trình đó.

Giải bất phương trình là tìm tập nghiệm của bất phương trình đó.

Ví dụ 1: Tập nghiệm của bất phương trình x > 2 là tập hợp các số lớn hơn 2, tức là tập hợp { x| x > 2 }.

Để dễ hình dung, ta biểu diễn tập hợp này trên trục số như hình vẽ sau:

Ví dụ 2: Tập nghiệm của bất phương trình x ≤ 7 là tập hợp các số nhỏ hơn hoặc bằng 7, tức là tập hợp { x| x ≤ 7 } .

Để dễ hình dung, ta biểu diễn tập hợp này trên trục số như hình vẽ sau:

3. Bất phương trình tương đương

Hai bất phương trình tương đương là hai bất phương trình có cùng tập nghiệm.

Kí hiệu là "⇔".

Ví dụ: Bất phương trình x > 3 và bất phương trình 6 < 2x có cùng tập nghiệm là { x| x > 3 }.

B. Bài tập tự luyện

Bài 1: Giải bất phương trình sau và biểu diễn nghiệm trên trục số

Hướng dẫn:

a) Ta có: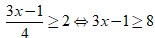 ⇔ 3x - 1 > 8

⇔ 3x ≥ 9 ⇔ x ≥ 3

Vậy x ≥ 3 là nghiệm của bất phương trình.

Ta biểu diễn tập nghiệm trên trục số như sau:

b) Ta có: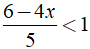 ⇔ 6 - 4x < 5

⇔ 4x > 1 ⇔ x > 1/4

Vậy x > 1/4 là nghiệm của bất phương trình đã cho.

Ta biểu diễn tập nghiệm trên trục số như sau:

Bài 2: Giải các bất phương trình sau:

a) 3x - 5 < 4

b) 3 - 4x ≥ 19

Hướng dẫn:

a) Ta có: 3x - 5 < 4 ⇔ 3x < 9 ⇔ x < 3

Vậy x < 3 là nghiệm của bất phương trình đã cho.

b) Ta có: 3 - 4x ≥ 19 ⇔ 3 - 19 ≥ 4x ⇔ - 16 ≥ 4x ⇔ x ≤ - 4

Vậy x ≤ - 4 là nghiệm của bất phương trình đã cho.