Cách tính độ dài đoạn thẳng trong hình thang hay, chi tiết
Cách tính độ dài đoạn thẳng trong hình thang hay, chi tiết
Tài liệu Cách tính độ dài đoạn thẳng trong hình thang hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.
A. Phương pháp giải.
Sử dụng:
- Tính chất về cạnh bên và đường chéo của hình thang cân: Trong hình thang cân, hai cạnh bên bằng nhau, hai đường chéo bằng nhau.
- Trong một tam giác, đối diện với hai góc bằng nhau là hai cạnh bằng nhau.
- Áp dụng định lý Py – ta -go.
B. Ví dụ minh họa
Ví dụ 1. Tính chiều cao của hình thang cân ABCD (AB//CD), biết rằng cạnh bên AD = 5cm, các cạnh đáy AB = 6cm và CD = 14cm.
Giải
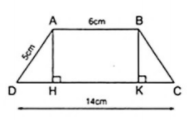
Kẻ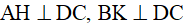 
thì AH//BK nên hình thang ABKH có hai cạnh bên song song.
Áp dụng nhận xét về hình thang có hai cạnh bên song song vào hình thang ABKH, ta được: AH = BK, HK = AB = 6cm.
Xét hai tam giác vuông ADH và BCK có:
AH = BK (cmt)
AD = BC (ABCD là hình thang cân)
Do đó: ΔADH= ΔBCK (cạnh huyền, cạnh góc vuông)
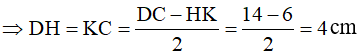
Áp dụng định lí Py –ta–go vào tam giác ADH vuông tại H, thu được:
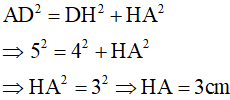
Vậy chiều cao hình thang cân là 3 cm.
Ví dụ 2. Một hình thang cân có đáy lớn dài 2,7 m. Cạnh bên dài 1 m, góc tạo bởi cạnh bên và đáy lớn bằng 600 . Tính độ dài đáy nhỏ.
Giải
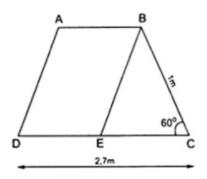
Giả sử ta có hình thang cân ABCD có đáy lớn DC = 2,7m, cạnh bên BC = 1m và
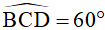
Kẻ BE//AD ta được hình thang ABED có hai cạnh bên BE, AD song song nên
AB = DE.
Áp dụng nhận xét hình thang có hai cạnh bên song song vào hình thang ABED, tính chất về cạnh, giả thiết vào hình thang cân ABCD ta được:
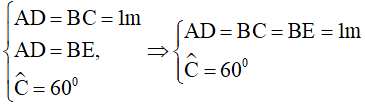
Suy ra ΔBCE là tam giác đều có cạnh EC = 1m.
Vậy đáy nhỏ AB = DE = DC – EC = 2,7 – 1 = 1,7 m.
Ví dụ 3. Cho hình thang cân MNPQ (MN//PQ) có góc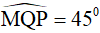 
và hai đáy có độ dài 12cm, 40cm. Diện tích của hình thang cân là?
Giải
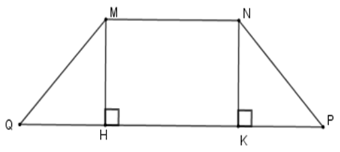
Kẻ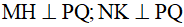 
tại H, K 
.
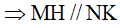Tứ giác MNKH có MN//HK nên MNKH là hình thang, lại có MH//NK
⇒ MN = HK; MH = NK (vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Xét 2 tam giác vuông MQH và NPK có:
MQ = NP (vì MNPQ là hình thang cân)
MH = NK (cmt)
Do đó: ΔMQH =ΔNPK (cạnh huyền, cạnh góc vuông)
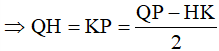
Mà HK = MN = 12cm nên
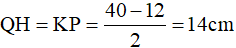
Mà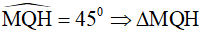 
vuông cân tại H ⇒ MH = QH = 14 cm.
Vậy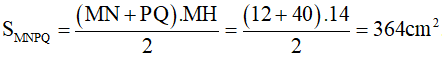 
Ví dụ 4. Cho hình thang cân ABCD có đáy nhỏ AB = 4cm, đường cao AH = 6cm và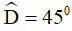 
. Độ dài đáy lớn CD bằng:
A. 12cm.
B. 16cm.
C. 18cm.
D. 20cm.
Giải
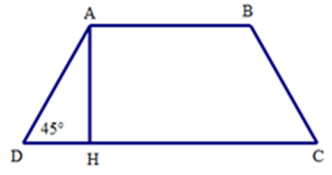
Ta có tam giác ADH vuông cân tại H vì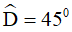 
. Do đó DH = AH = 6cm.
Mà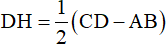 
(chứng minh tương tự ví dụ 3).
Suy ra CD = 2DH + AB = 2.6 + 4 = 16(cm).
Vậy CD = 16cm.
Đáp án: B.
Ví dụ 5. Cho hình thang cân ABCD có đáy nhỏ AB = 4cm, đáy lớn CD = 10cm, cạnh bên BC = 5cm thì đường cao AH bằng?
Giải
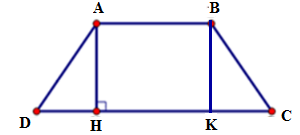
Kẻ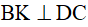 
tại K.
Hình thang ABKH có hai cạnh bên AH//BK (cùng vuông góc với CD) nên AH = BK;
AB = HK (vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau).
Xét 2 tam giác vuông AHD và BKC có
AH = BK (cmt)
AD = BC (ABCD là hình thang cân)
Do đó: ΔAHD=ΔBKC (cạnh huyền, cạnh góc vuông)
Suy ra
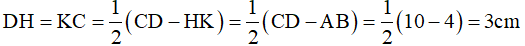
Do ABCD là hình thang cân nên AD = BC = 5cm
Áp dụng định lý Py-ta-go vào tam giác ADH vuông tại H ta có:
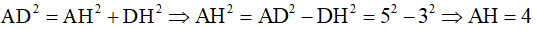
Vậy AH = 4cm.
Ví dụ 6. Hình thang cân ABCD có đường chéo BD vuông góc với cạnh bên BC và DB là tia phân giác của góc D. Tính chu vi của hình thang, biết BC = 4cm.
Giải
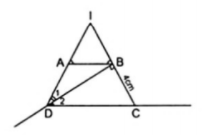
Gọi I là giao điểm của AD và BC thu được tam giác IDC.
Ta có AB//CD nên: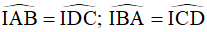 
(các góc ở vị trí đồng vị)
Mà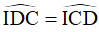 
(do ABCD là hình thang cân)
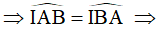Tam giác IAB cân tại I ⇒ IA = IB.
Mà IA + AD = ID; IB + BC = IC, suy ra ID = IC.
Theo giả thiết DB vừa là tia phân giác của góc D vừa là đường cao nên tam giác IDC cân tại D mà ID = IC suy ra nó là tam giác đều cạnh DC = CI = 2BC = 8cm.
Ta có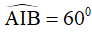 
(tam giác IDC đều), suy ra tam giác IAB là tam giác đều nên AB = IB = BC = 4cm.
Vậy chu vi hình thang cân là AB + BC + CD + AD = 4 + 4 + 8 + 4 = 20 cm.
