Chứng minh hai đường thẳng song song, ba điểm thẳng hàng hay, chi tiết

Chứng minh hai đường thẳng song song, ba điểm thẳng hàng hay, chi tiết

Tài liệu Chứng minh hai đường thẳng song song, ba điểm thẳng hàng hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải.

• Vẽ thêm đường trung bình.
• Áp dụng định lí đường trung bình của tam giác, của hình thang.
• Sử dụng tiên để Ơ-clit về đường thẳng song song: Qua một điểm ở ngoài

một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó hoặc sử dụng tính chất nếu một góc là góc bẹt thì hai cạnh của góc ấy là hai tia đối nhau hay hai cạnh của góc này nằm trên một đường thẳng.

B. Ví dụ minh họa

Ví dụ 1. Cho , kéo dài trung tuyến BD đến F sao cho DF = BD và trung tuyến CE đến G sao cho EG = CE. Chứng minh ba điểm G, A, F thẳng hàng.

Giải

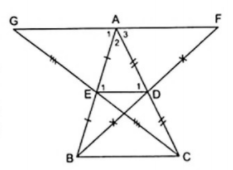
Vì BD, CE là hai trung tuyến của ΔABC theo giả thiết nên D, E lần lượt là trung điểm của AC, AB hay AD = DC, AE = EB.

Từ giả thiết DF = BD, EG = CE suy ra ED là đường trung bình của hai tam giác ACG và ABF.

Áp dụng định lí đường trung bình vào hai tam giác trên, ta được:

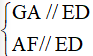
⇒ ba điểm G, A, F thẳng hàng (vì qua điểm A nằm ngoài đường thẳng ED chỉ có một đường thẳng song song với ED).

Ta cũng có thể giải thích lí do trên bằng cách khác:

Ta có 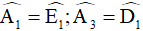vì là góc so le trong của ED//GA và ED//AF.

Áp dụng tính chất về góc vào ΔAED, thu được:

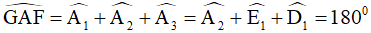hay góc GAF là góc bẹt suy ra AG và AF là hai tia đối nhau tức là G, A, F thẳng hàng.

Ví dụ 2. Từ đỉnh A của ΔABC lần lượt kẻ các đường vuông góc AK, AH xuống các đường phân giác củ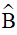a và 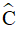. Chứng minh HK//BC.

Giải

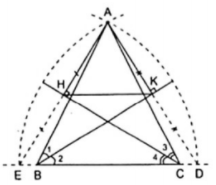
Gọi giao điểm của AH, AK với đường thẳng BC lần lượt là E và D.

Từ giả thiết suy ra BK vừa là đường phân giác vừa là đường cao của ΔABD nên tam giác này cân tại B. CH vừa là đường phân giác vừa là đường cao của ΔAEC nên tam giác này cân tại C. Theo tính chất của tam giác cân thì CH, BK là các đường trung tuyến của ΔAEC và ΔABD hay AH = HE, AK = KD, nên HK là đường trung bình của ΔAED.

Áp dụng định lí đường trung bình vào ΔAED thu được HK//ED.

Vậy HK//BC.

Ví dụ 3. Hình thang ABCD có đáy AB, CD. Gọi E, F, K thứ tự là trung điểm của AD, BD, BC. Chứng minh ba điểm E, F, K thẳng hàng.

Giải

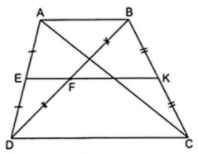
Vì E, F, K thứ tự là trung điểm của AD, BD, BC theo giả thiết nên EF là đường trung bình của tam giác ABD, EK là đường trung bình của hình thang ABCD.

Áp dụng định lí đường trung bình vào tam giác ABD và hình thang ABCD, ta có:

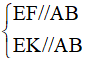
⇒E,K,F là ba điểm thẳng hàng. Vì từ điểm E ở ngoài đường thẳng AB chỉ kẻ được một đường thẳng song song với nó.

Ví dụ 4. Cho ΔABC có các đường trung tuyến BD, CE cắt nhau tại G. Gọi H, I lần lượt là trung điểm của GB, GC. Chứng minh DE//HI và DE = HI.

Giải

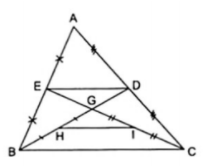
Từ giả thiết ta có ED, HI lần lượt là các đường trung bình của hai tam giác

ABC và GBC. Áp dụng định lí đường trung bình vào hai tam giác này, ta được:

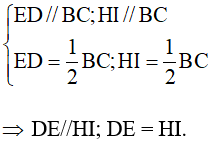
Ví dụ 5. Chứng minh rằng trong một hình thang, trung điểm hai cạnh bên, trung điểm hai đường chéo là bốn điểm thẳng hàng.

Giải

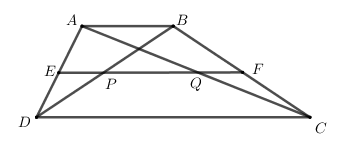
Xét hình thang ABCD (AB//CD).

Gọi E, P, Q, F lần lượt là trung điểm của AD, BD, AC, BC thì EF, EP, EQ thứ tự là các đường trung bình của hình thang ABCD, tam giác ABD và tam giác ACD.

Áp dụnh định lí đường trung bình vào các tam giác và vào hình thang, ta được: EP//AB//CD; EQ//CD//AB; EF//AB//CD.

Suy ra bốn điểm E, P, Q, F thẳng hàng (vì từ điểm E ở ngoài hai đường thẳng AB//CD chỉ kẻ được một đường thẳng song song với hai đường thẳng đó).