Dạng bài tập chứng minh bất đẳng thức diện tích

Dạng bài tập chứng minh bất đẳng thức diện tích

Tài liệu Dạng bài tập chứng minh bất đẳng thức diện tích Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

Dạng bài: Chứng minh bất đẳng thức diện tích

A. Phương pháp giải

+) Sử dụng tính chất diện tích đa giác.

+) Số đo diện tích của một hình luôn là một số dương.

B. Ví dụ minh họa

Câu 1: Cho ΔABC vuông tại A có AH là đường cao. Trên AB, AC lấy K, L sao cho AK = AL = AH. Chứng minh rằng .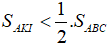

Lời giải:

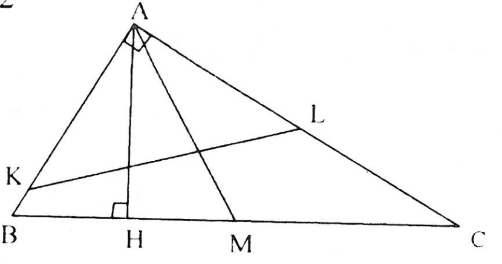
Ta có:

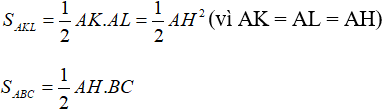
Gọi M là trung điểm của BC, ta có

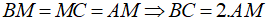
Mặt khác 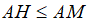(quan hệ đường vuông góc và đường xiên)

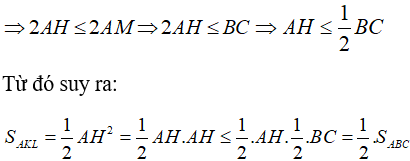
Đẳng thức xảy ra khi 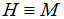hay ΔABC vuông cân.

Câu 2: Cho lục giác lồi ABCDEF có các cặp cạnh đối song song.

Chứng minh

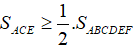
Lời giải:

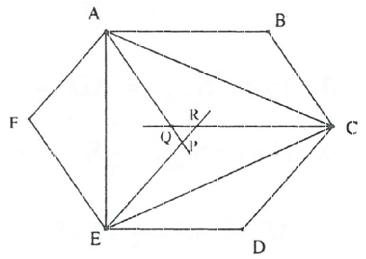
Vẽ hình bình hành ABCQ; CDER; AFEP

Ta có:

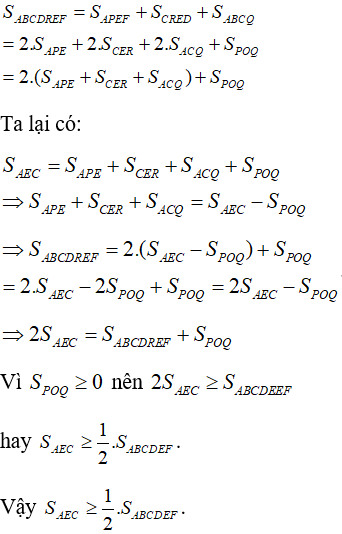
C. Bài tập tự luyện

Câu 1: Cho một ngũ giác. Có ba đường thẳng 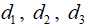cắt nhau tạo ba điểm A, B, C thuộc miền trong ngũ giác sao cho mỗi đường thẳng chia ngũ giác thành hai phần có diện tích bằng nhau. Chứng minh diện tích tam giác ABC nhỏ hơn 1/4 diện tích ngũ giác đã cho.

Câu 2: Cho lục giác lồi ABCDEF có các cặp cạnh đối song song và có diện tích bằng S. Chứng minh

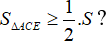
Câu 3: Chứng minh rằng hai hình chữ nhật bằng nhau kích thước axb được xếp sao cho chúng cắt nhau tại 8 điểm thì diện tích phần chung lớn hơn nửa diện tích một hình chữ nhật.