Tìm các yếu tố song song, vuông góc trong hình lăng trụ đứng

Tìm các yếu tố song song, vuông góc trong hình lăng trụ đứng

Tài liệu Tìm các yếu tố song song, vuông góc trong hình lăng trụ đứng Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

Dạng bài: Tìm các yếu tố song song, vuông góc trong hình lăng trụ đứng

A. Phương pháp giải

B. Ví dụ minh họa

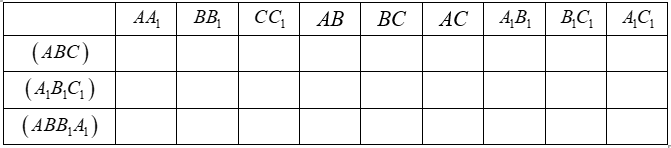
Câu 1: ABC.A₁B₁C₁ là một lăng trụ đứng tam giác.

a) Trong hình lăng trụ đó hãy chỉ ra những cặp mặt phẳng song song với nhau.

b) Trong hình lăng trụ đó hãy chỉ ra những cặp mặt phẳng vuông góc với nhau.

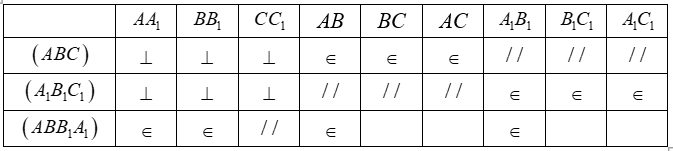
c) Sử dụng kí hiệu 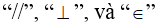điền vào các ô trong bảng sau:

Lời giải:

a) Ta chỉ có .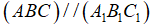

b) Ta có:

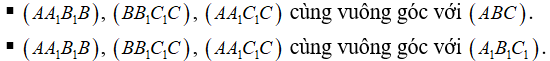
c) Ta có:

Câu 2: Cho hình lăng trụ đứng ABCD.A₁B₁C₁D₁ có đáy ABCD là hình thang cân (AB//CD) có AC vuông góc với BD.

a) Đường thẳng BD và A₁C có cắt nhau không? Vì sao?

b) Đường thẳng AD song song với những mặt phẳng nào?

c) Đường thẳng AC vuông góc với những mặt phẳng nào?

d) Trong hình lăng trụ đó hãy chỉ ra những cặp mặt phẳng song song với nhau.

e) Trong hình lăng trụ đó hãy chỉ ra những cặp mặt phẳng vuông góc với nhau.

Lời giải:

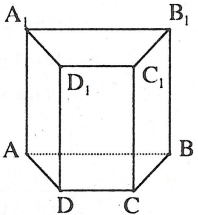a) Đường thẳng BD và A₁C không cắt nhau, bởi nếu chúng cắt nhau thì 4 điểm B, C, D, A₁ cùng thuộc một mặt phẳng

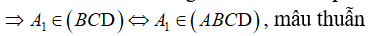
b) Ta có:

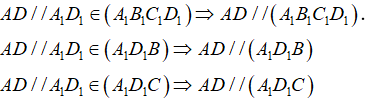
Vậy, có 3 mặt phẳng (A₁B₁C₁D₁), (A₁D₁B), (A₁D₁C) song song với AD.

c) Ta có:

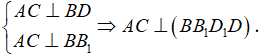
Vậy có duy nhất mặt phẳng (BB₁D₁D) vuông góc với AC.

d) Ta có các cặp mặt phẳng song song với nhau là:

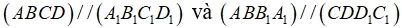
e) Dựa trên tính chất của hình lăng trụ đứng ta có ngay các mặt phẳng vuông góc với hai đáy (ABCD) và (A₁B₁C₁D₁) là:

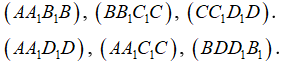
Mặt khác:

- Vì 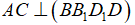nên các mặt phẳng chứa AC đều vuông góc với mặt phẳng (BB₁D₁D), do đó ta có:

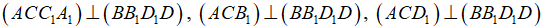
- Vì 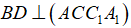nên các mặt phẳng chứa BD đều vuông góc với mặt phẳng (ACC₁A₁), do đó ta có:

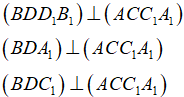
- Vì 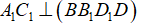nên các mặt phẳng chứa C₁A₁ đều vuông góc với mặt phẳng (BB₁D₁D), do đó ta có thêm:

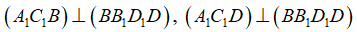
- Vì 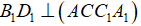nên các mặt phẳng chứa BD đều vuông góc với mặt phẳng (ACC₁A₁), do đó ta có thêm:

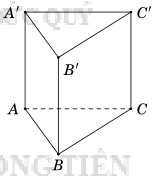
Câu 3: Cho hình lăng trụ đứng ABC.A'B'C' , đáy ABC là tam giác vuông tại A.

a) Chứng minh rằng .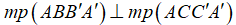

b) Gọi M là một điểm bất kì trên cạnh B'C'. Chứng minh rằng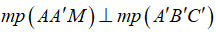

c) Xác định vị trí của điểm M trên cạnh B'C' để độ dài AM nhỏ nhất.

Lời giải:

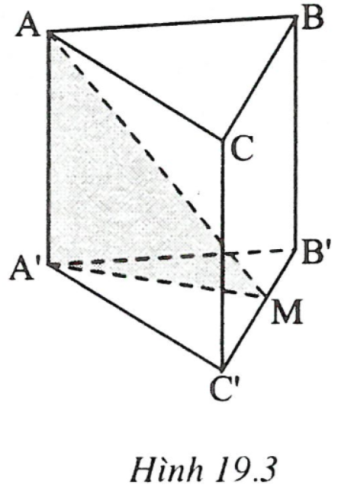a) Ta có:

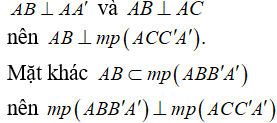
b) Hình lăng trụ ABC.A'B'C' là hình lăng trụ đứng nên

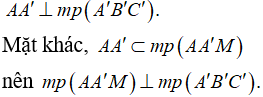
Vậy để độ dài AM nhỏ nhất thì M phải là hình chiếu của A trên B'C'.

C. Bài tập tự luyện

Câu 1: Cho hình lăng trụ đứng ABC. A’B’C’ đáy là tam giác ABC vuông tại A. Chứng minh rằng:

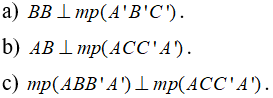
Câu 2: Cho lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thang vuông 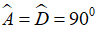. Hãy cho biết

a) Các cạnh song song với AB.

b) Các cạnh vuông góc với AB tại A.

c) Các cạnh song song với mp(DCC'D').

d) Các cạnh vuông góc với mp(DCC'D').

e) Mặt phẳng song song với mp(DCC'D').

Câu 3: Cho hình lăng trụ đứng ABC. A’B’C’. Gọi E và G lần lượt là trọng tâm của tam giác ABB' và ACC'. Trong mặt bên ABB'A' vẽ EM//BB' (M∈AB) Trong mặt bên ACC'A' vẽ GN//CC' (N∈AC)

Chứng minh rằng mp(MNGE) // mp(BCC'B')

Câu 4: Cho hình lăng trụ đứng ABC. A’B’C’ có cạnh đáy AB=AC=10cm và BC=12cm. Gọi M là trung điểm của B'C'. Chứng minh rằng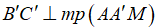

Câu 5: Cho hình lăng trụ đứng tam giác ABC.A’B’C’. Gọi M, N, P, Q lần lượt là trọng tâm của tam giác ABC, ABB’, A’B’C’, A’C’C. Chứng minh MNPQ là hình bình hành.

Câu 6: Cho hình lăng trụ ABCD. A’B’C’D’ có đáy là hình thoi. Gọi O và O’ là tâm các mặt đáy. Chứng minh rằng:

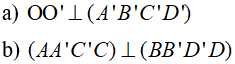
Câu 7: Cho lăng trụ đứng ABC. A’B’C’. Gọi M, N lần lượt là trung điểm của BB’, CC’ và G là trọng tâm của tam giác A’B’C’. Chứng minh (B’A’N)//(MC’G).
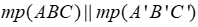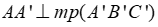