Các dạng bài tập Toán 8 Chương 1: Tứ giác chọn lọc

Các dạng bài tập Toán 8 Chương 1: Tứ giác chọn lọc

Haylamdo biên soạn và sưu tầm Các dạng bài tập Chương 1: Tứ giác chọn lọc môn Toán lớp 8 sẽ giúp học sinh nắm vững lý thuyết, biết cách làm các dạng bài tập từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi môn Toán 8.

Mục lục Toán 8 Chương 1: Tứ giác

I/ Lý thuyết & Bài tập theo bài học

• Lý thuyết Bài 1: Tứ giác
• Bài tập Bài 1: Tứ giác
• Lý thuyết Bài 2: Hình thang
• Bài tập Bài 2: Hình thang
• Lý thuyết Bài 3: Hình thang cân
• Bài tập Bài 3: Hình thang cân
• Lý thuyết Bài 4: Đường trung bình của tam giác, của hình thang
• Bài tập Bài 4: Đường trung bình của tam giác, của hình thang
• Lý thuyết Bài 5: Dựng hình bằng thước và compa. Dựng hình thang
• Lý thuyết Bài 6: Đối xứng trục
• Bài tập Bài 6: Đối xứng trục
• Lý thuyết Bài 7: Hình bình hành
• Bài tập Bài 7: Hình bình hành
• Lý thuyết Bài 8: Đối xứng tâm
• Bài tập Bài 8: Đối xứng tâm
• Lý thuyết Bài 9: Hình chữ nhật
• Bài tập Bài 9: Hình chữ nhật
• Lý thuyết Bài 10: Đường thẳng song song với một đường thẳng cho trước
• Bài tập Bài 10: Đường thẳng song song với một đường thẳng cho trước
• Lý thuyết Bài 11: Hình thoi
• Bài tập Bài 11: Hình thoi
• Lý thuyết Bài 12: Hình vuông
• Bài tập Bài 12: Hình vuông
• Tổng hợp Lý thuyết & Trắc nghiệm Chương 1 Hình học 8

II/ Các dạng bài tập

• Các dạng bài tập về góc trong tứ giác
• Các dạng bài tập về hình thang, hình thang vuông, hình thang cân
• Các dạng toán về đối xứng trục, đối xứng tâm
• Các dạng bài tập về đường trung bình của tam giác, hình thang
• Các dạng toán về hình bình hành
• Các dạng toán về hình chữ nhật
• Các dạng bài tập về hình thoi
• Các dạng toán về hình vuông
• Các dạng toán về đường thẳng song song với đường thẳng cho trước

• Cách nhận biết các tứ giác hay, chi tiết
• Tính số đo góc trong tứ giác hay, chi tiết
• Cách vẽ tứ giác khi biết 5 yếu tố hay, chi tiết
• Chứng minh hệ thức trong tứ giác hay, chi tiết
• Cách nhận biết hình thang, hình thang vuông hay, chi tiết
• Cách nhận biết hình thang cân hay, chi tiết
• Cách tính số đo góc trong hình thang hay, chi tiết
• Cách tính độ dài đoạn thẳng trong hình thang hay, chi tiết
• Chứng minh hai đoạn thẳng, hai góc bằng nhau hay, chi tiết
• Tính độ dài đoạn thẳng dựa vào đường trung bình của tam giác, hình thang
• Chứng minh hai đường thẳng song song, ba điểm thẳng hàng hay, chi tiết
• Cách dựng hình thang bằng thước và compa hay, chi tiết
• Cách dựng hình tam giác bằng thước và compa hay, chi tiết
• Cách vẽ hình đối xứng của một hình cho trước hay, chi tiết
• Tìm hình có trục đối xứng – Tìm trục đối xứng của một hình
• Chứng minh hai đoạn thẳng bằng nhau, hai góc bằng nhau chi tiết
• Chứng minh hai điểm đối xứng qua một đường thẳng hay, chi tiết
• Tìm vị trí của một điểm để tổng hai đoạn thẳng ngắn nhất
• Chứng minh hai góc bằng nhau, tính số đo góc trong hình bình hành
• Chứng minh hai đoạn thẳng bằng nhau trong hình bình hành
• Chứng minh ba điểm thẳng hàng, ba đường thẳng đồng qui trong hình bình hành
• Cách chứng minh tứ giác là hình bình hành hay, chi tiết
• Cách vẽ hình đối xứng của một hình cho trước hay, chi tiết
• Tìm hình có tâm đối xứng – Tìm tâm đối xứng của một hình
• Chứng minh hai đoạn thẳng hoặc hai góc bằng nhau sử dụng đối xứng tâm
• Chứng minh hai điểm đối xứng qua một điểm hay, chi tiết
• Cách chứng minh tứ giác là hình chữ nhật hay, chi tiết
• Tìm điều kiện của hình A để hình B trở thành hình chữ nhật
• Chứng minh hai đoạn thẳng, hai góc bằng nhau trong hình chữ nhật
• Chứng minh hai đường thẳng vuông góc dựa vào hình chữ nhật
• Chứng tỏ một điểm di động trên 1 đường thẳng song song với 1 đường thẳng cho trước
• Cách chia đoạn thẳng AB cho trước thành nhiều phần bằng nhau
• Cách chứng minh tứ giác là hình thoi hay, chi tiết
• Tìm điều kiện của hình A để hình B trở thành hình thoi
• Chứng minh hai đoạn thẳng, hai góc bằng nhau trong hình thoi
• Chứng minh hai đường thẳng vuông góc dựa vào hình thoi
• Cách chứng minh tứ giác là hình vuông hay, chi tiết
• Tìm điều kiện của hình A để hình B trở thành hình vuông
• Chứng minh hai đoạn thẳng, hai góc bằng nhau trong hình vuông
• Chứng minh hai đường thẳng vuông góc dựa vào hình vuông

Cách nhận biết các tứ giác hay, chi tiết

A. Phương pháp giải

Dựa vào định nghĩa:

• Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
• Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác (từ nay, khi nói đến tứ giác mà không chú thích gì thêm, ta hiểu đó là tứ giác lồi).

B. Ví dụ minh họa

Ví dụ 1. Hình nào trong các hình sau là tứ giác?

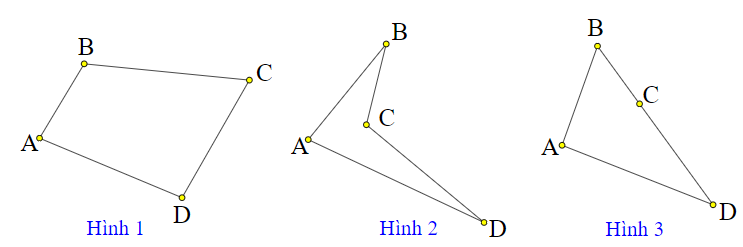
Giải

Hình 1: Tứ giác lồi.

Hình 2: Tứ giác không lồi.

Hình 3: Không phải là tứ giác (tam giác).

Ví dụ 2. Trong hình sau có bao nhiêu hình tứ giác?

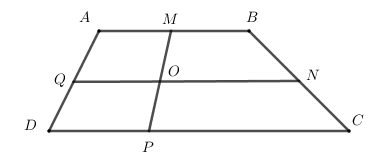
Giải

Có 9 hình tứ giác là: ABCD, ABNQ, QNCD, AMPD, MBCP, AMOQ, QOPD, MBNO, ONCP.

Ví dụ 3. Trong các hình sau có bao nhiêu tứ giác lồi?

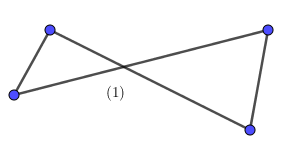
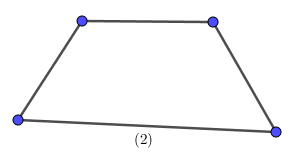
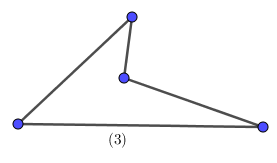
Giải

Có tất cả 2 tứ giác lồi là tứ giác (2) và tứ giác (4) vì tất cả các cạnh luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác.

Tứ giác (1) và (3) là tứ giác không lồi.

Ví dụ 4. Số tứ giác trong các hình sau là bao nhiêu?

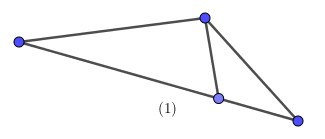
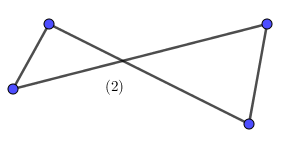
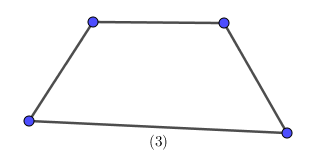
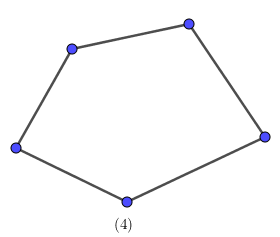
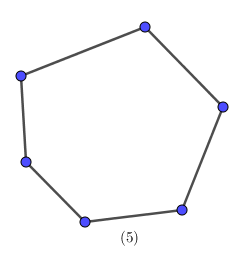
Ta có:

(1): tam giác

(2): tứ giác không lồi

(3): tứ giác lồi

(4): ngũ giác

(5): lục giác

Vậy có tất cả 2 hình tứ giác.

Tính số đo góc trong tứ giác hay, chi tiết

A. Phương pháp giải.

Sử dụng:

• Tính chất về góc của một tam giác: Tổng các góc của một tam giác bằng .
• Tính chất về góc của một tứ giác: Tổng các góc của một tứ giác bằng .
• Khái niệm: Hai góc bù nhau là hai góc có tổng bằng .
• Tính chất của dãy tỉ số bằng nhau:

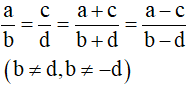
B. Ví dụ minh họa

Ví dụ 1. Tìm x ở hình 4a và hình 4b.

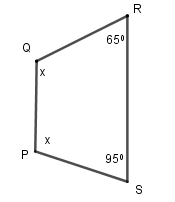
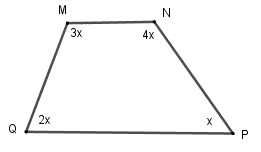
a) b)

Giải

a) Áp dụng tính chất về tổng các góc cho tứ giác PQRS, ta được:

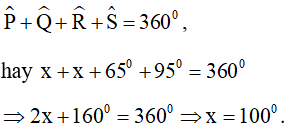
b) Áp dụng tính chất về tổng các góc cho tứ giác MNPQ ta được:

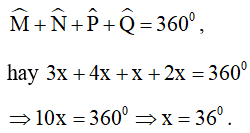
Ví dụ 2. Cho tứ giác ABCD có 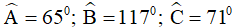. Số đo góc ngoài tại đỉnh D bằng bao nhiêu?

Giải

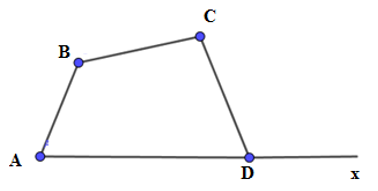
Kéo dài tia AD ta được tia Ax, suy ra 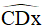là góc ngoài đỉnh D.

Áp dụng tính chất về tổng các góc cho tứ giác ABCD có:

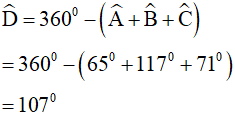
Ta thấy góc ngoài tại đỉnh D chính là góc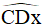

Vì 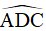và 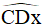là hai góc kề bù nên

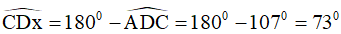
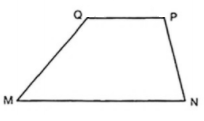
Ví dụ 3. Cho tứ giác MNPQ biết:

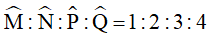
a) Tính các góc của tứ giác.

b) Gọi R là giao điểm của MQ với NP. Chứng minh rằng MN//PQ.

c) Tính các góc của tam giác PQR.

Giải

a) Viết lại giả thiết thành

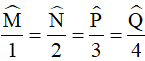
Áp dụng tính chất của dãy tỉ số bằng nhau và tính chất về tổng các góc vào tứ giác MNPQ ta có:

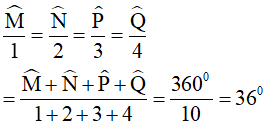
Vậy

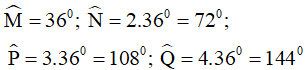
b)

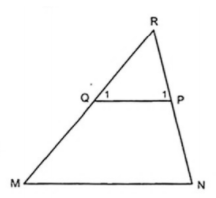
Vì 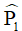là góc ngoài của tứ giác MNPQ tại đỉnh P, nên:

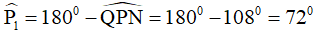
Do đó 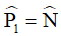(cặp góc ở vị trí đồng vị bằng nhau).

Vậy .

c)

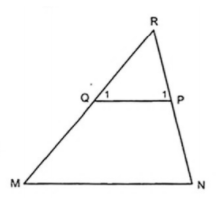
Theo câu b) thì .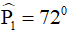

Ta có 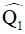là góc ngoài của tứ giác MNPQ tại đỉnh Q.

Nên

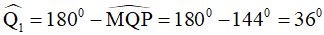
Áp dụng tính chất về tổng các góc vào tam giác PQR , ta có:

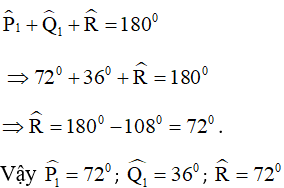
Cách vẽ tứ giác khi biết 5 yếu tố hay, chi tiết

A. Phương pháp giải.

Bước 1: Chọn một tam giác biết ba yếu tố vẽ trước để xác định ba đỉnh của tứ giác.

Bước 2: Lợi dụng một cạnh của tam giác đã vẽ với hai yếu tố còn lại của tam giác thứ hai để xác định đỉnh thứ 4.

B. Ví dụ minh họa

Ví dụ 1. Vẽ tứ giác ABCD với các số đo như hình vẽ.

Giải

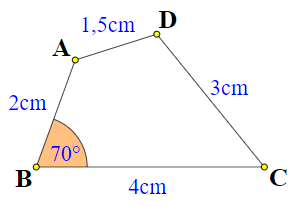
Bước 1: Vẽ biết hai cạnh BA = 2cm; BC = 4cm và 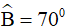theo các bước sau:

• Vẽ đoạn thẳng BC = 4cm

• Vẽ tia Bx sao cho

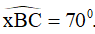
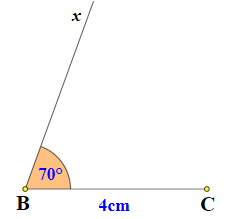
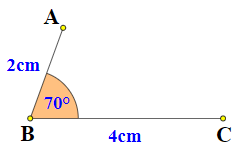
• Trên tia Bx lấy điểm A, sao cho AB = 2cm.

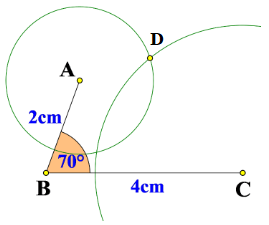
Bước 2: Vẽ đường tròn tâm A bán kính 1,5cm và đường tròn tâm C bán kính 3cm. Hai đường tròn này cắt nhau tại D.

Bước 3: Nối các đỉnh A, B, C, D ta có tứ giác ABCD cần vẽ.

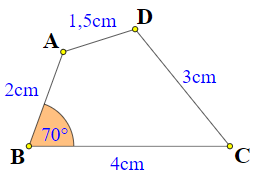
Ví dụ 2. Vẽ tứ giác ABCD trong trường hợp sau biết: Bốn cạnh AB = 2cm; BC = 3cm; CD = 2,5cm; DA = 2cm và đường chéo AC = 4cm.

Bước 1: Vẽ tam giác ABC biết ba yếu tố AB = 2cm; BC = 3cm; AC = 4cm theo các bước sau:

• Vẽ đoạn thẳng AC = 4cm.

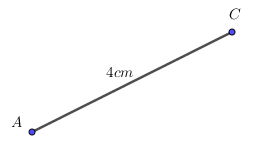
• Vẽ đường tròn tâm A bán kính 2cm và đường tròn tâm C bán kính 3cm. Hai đường tròn này cắt nhau tại B.

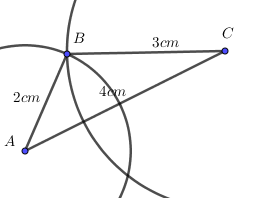
Bước 2: Vẽ tam giác ACD biết ba yếu tố AD = 2cm; CD = 2,5cm; AC = 4cm

• Giữ đường tròn tâm A bán kính 2cm và vẽ đường tròn tâm C bán kính 2,5cm. Hai đường tròn này cắt nhau tại D.

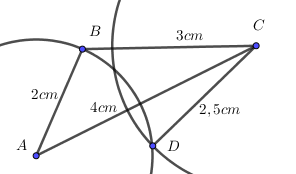
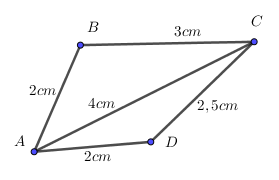
Bước 3: Nối các đỉnh A, B, C, D ta có tứ giác ABCD cần vẽ.

Ví dụ 3. Vẽ tứ giác ABCD trong trường hợp sau, biết: Bốn cạnh AB = 3,5 cm; BC = 4cm; CD = 4,5cm và đường chéo AC = 5,5cm và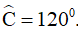

Giải

Bước 1: Vẽ tam giác ABC biết ba yếu tố AB = 3,5 cm; BC = 4cm; AC = 5,5cm theo các bước sau:

• Vẽ đoạn thẳng AC = 5,5cm.

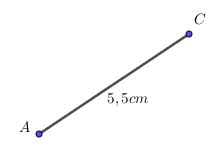
• Vẽ đường tròn tâm A bán kính 3,5cm và đường tròn tâm C bán kính 4cm. Hai đường tròn này cắt nhau tại B.

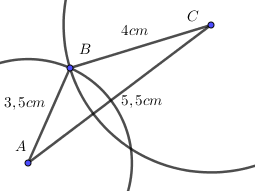
Bước 2: Vẽ 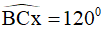, trên tia Cx lấy điểm D sao cho CD = 4,5cm.

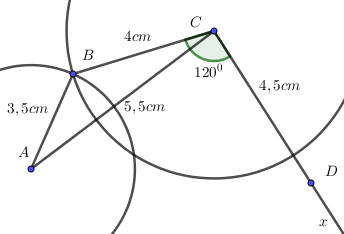
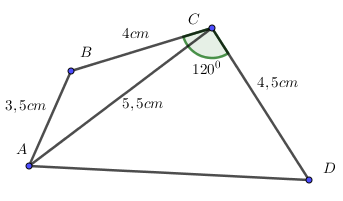
Bước 3: Nối các đỉnh A, B, C, D ta có tứ giác ABCD cần vẽ.

....................................

....................................

....................................