Cách giải phương trình đưa được về dạng ax + b = 0 cực hay, có đáp án
Cách giải phương trình đưa được về dạng ax + b = 0 cực hay, có đáp án
Tài liệu Cách giải phương trình đưa được về dạng ax + b = 0 cực hay, có đáp án Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải
- Dùng quy tắc bỏ dấu ngoặc hay quy đồng khử mẫu (không chứa ẩn) để đưa phương trình về dạng ax + b = 0 hay ax = -b.
- Sử dụng hai quy tắc biến đổi phương trình để giải.
+ Qui tắc chuyển vế: Trong một phương trình, ta có thể chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó.
+ Qui tắc nhân: Trong một phương trình, ta có thể nhân cả hai vế với cùng một số khác 0.
B. Ví dụ minh họa
Ví dụ 1: Giải các phương trình sau
a, 5 – (6 – x) = 4(3 – 2x)
b) 4(x – 4) = -7x +17
Hướng dẫn giải:
a, 5 – (6 – x) = 4(3 – 2x)
⇔ 5 – 6 + x = 12 – 8x
⇔ x + 8x = 12 – 5 + 6
⇔ 9x = 13
⇔ x = 13/9
Vậy phương trình có một nghiệm x = 13/9.
b) 4(x – 4) = -7x +17
⇔ 4x - 16 = -7x + 17
⇔ 4x + 7x = 17 + 16
⇔ 11x = 33
⇔ x = 3
Phương trình có tập nghiệm S = { 3}
Ví dụ 2: Giải các phương trình sau
a, 2(x – 3) = -3(x – 1) + 7.
b, 4(3x – 2) – 3(x - 4) = 7x + 20.
Hướng dẫn giải:
a, 2(x – 3) = -3(x – 1) + 7.
⇔ 2x – 6 = -3x + 3 + 7
⇔ 5x = 16
⇔ 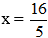
Vậy phương trình có tập nghiệm S = {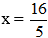
b, 4(3x – 2) – 3(x - 4) = 7x + 20.
⇔ 12x – 8 – 3x + 12 = 7x + 20
⇔ 9x – 7x = 20 + 8 – 12
⇔ 2x = 16
⇔ x = 8
Vậy phương trình có tập nghiệm S = { 8}
Ví dụ 3: Giải các phương trình sau:
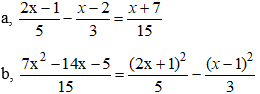
Hướng dẫn giải:
a, 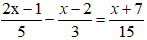
⇔ 3(2x – 1) – 5(x - 2) = x + 7
⇔ 6x – 3 – 5x + 10 = x + 7
⇔ x – x = 7- 7
⇔ 0x = 0 (pt thỏa mãn với mọi x)
Vậy phương trình đã cho có vô số nghiệm.
b, 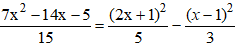
⇔ 7x2 – 14x – 5 = 3(2x + 1)2 – 5(x – 1)2
⇔ 7x2 – 14x – 5 = 3(4x2 + 4x + 1) – 5(x2 – 2x + 1)
⇔ 7x2 – 14x – 5 = 12x2 + 12x + 3 – 5x2 + 10x – 5
⇔ 7x2 – 14x - 7x2 - 22x = 3 – 5 + 5
⇔ -36 x = 3
⇔ 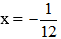
Vậy phương trình đã cho có một nghiệm 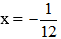
C. Bài tập vận dụng
Bài 1: Phương trình 5 - (2 – x) = 4(3 – 2x) có tập nghiệm là:
A. S = { 1}
B. {2}
C. {-1}
D. {-2}.
Đáp án: A.
5 - (2 – x) = 4(3 – 2x) ⇔ 5 – 2 + x = 12 - 8x ⇔ x + 8x = 12 – 3⇔ 9x = 9 ⇔ x = 1
Vậy phương trình có nghiệm x = 1.
Bài 2: Phương trình 5(x – 3) - 4 = 2(x – 1) +7 có tập nghiệm là:
A. S = { 6}
B. {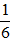
C. {8}
D. {-8}.
Đáp án: C.
5(x – 3) - 4 = 2(x – 1) +7 ⇔ 5x – 15 – 4 = 2x – 2+ 7
⇔ 5x – 2x = 5 + 19 ⇔ 3x = 24 ⇔ x = 8
Vậy phương trình có nghiệm x = 8.
Bài 3: Phương trình 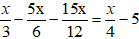

Đáp án: C.
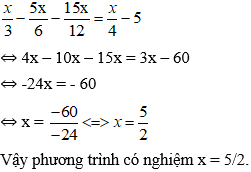
Bài 4: Giá trị x = 4 là nghiệm của phương trình nào trong các phương trình sau:
A. 7 – 3x = 9 - x
B. 2x – (3 – 5x) = 2(x + 3)
B. C(3x + 1) + 4 = 5(x + 2)
D. (3x + 2)2 – (3x – 2)2 = 5x + 3
Đáp án: B
Cách 1: Thay x = 4 vào các phương trình ta được:
A. 7 – 3.4 ≠ 9 - 4 ⇔ -5 ≠ 5
B. 2(3.4 + 1) + 4 = 5(4 + 2) ⇔ 30 = 30
C. 2.4 – (3 – 5.4) ≠ 2(4 +3) ⇔ 25 ≠ 14
D. (3.4+2)2 – (3.4 – 2)2 ≠ 5.4 + 3 ⇔ 96 ≠ 23
Cách 2:
Giải các phương trình ta được
A. 7 – 3x = 9 - x ⇔ -3x + x = 9 - 7 ⇔ -2x = 2 ⇔ x = -1
B. 2(3x + 1) + 4 = 5(x + 2) ⇔ 6x + 2 + 4 = 5x + 10 ⇔ x = 10 -2 – 4⇔ x = 4
C. 2x – (3 – 5x) = 2(x +3) ⇔ 2x – 3+ 5x = 2x + 6⇔ 5x = 6 + 3 ⇔ x = 9/5
D. (3x + 2)2 – (3x – 2)2 = 5x + 3 ⇔ 24x = 5x + 3 ⇔ 19x = 3 ⇔ x = 3/19.
Vậy x = 4 là nghiệm của phương trình 2(3x + 1) + 4 = 5(x + 2).
Bài 5: Phương trình 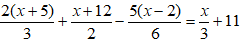
A. S = {1}
B. {-1}
C. S = ∅
D. S = R.
Đáp án: D
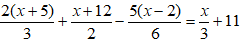
⇔ 4(x + 5) + 3(x + 12) - 5(x – 2) = 2x + 66
⇔ 4x + 20 + 3x + 36 – 5x + 10 = 2x + 66
⇔ 0x = 0 (thỏa mãn mọi giá trị của x)
Vậy phương trình đã cho có vô số nghiệm.
Bài 6: Giải các phương trình sau:
a, 3x – 2 = 5(x + 1)
b, 2x –(5x + 3) = 4(3x – 1) -7
Hướng dẫn giải:
a, 3x – 2 = 5(x + 1) ⇔ 3x – 2 = 5x + 5 ⇔ 3x – 5x = 5 +2 ⇔ -2x = 7 ⇔ x = -3,5
Vậy phương trình có nghiệm x = -3,5.
b, 2x –(5x + 3) = 4(3x – 1) -7 ⇔ 2x – 5x – 3 = 12x- 4 – 7 ⇔ - 15x = -8 ⇔ x = 8/15
Vậy phương trình có nghiệm x = 8/15.
Bài 7: Giải các phương trình sau:
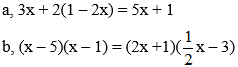
Hướng dẫn giải:
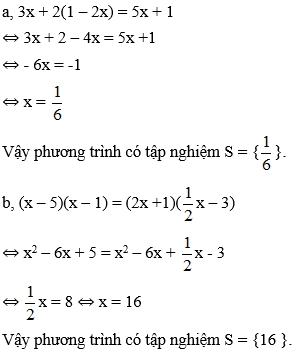
Bài 8: Giải các phương trình sau:
a, 3(x – 2)2 + 9(x – 1) = 3(x2 + x – 3)
b, (x + 1)(x2 – x +1) -2x = x(x - 1)(x + 1).
Hướng dẫn giải:
a, 3(x – 2)2 + 9(x – 1) = 3(x2 + x – 3)
⇔ 3x2 – 12x + 12 + 9x – 9 = 3x2 + 3x - 9
⇔ -6x = -12
⇔ x = 2
Vậy phương trình có tập nghiệm S = { 2 }.
b, (x + 1)(x2 – x + 1) - 2x = x(x - 1)(x + 1) ⇔ x3 – x2 + x + x2 – x + 1 – 2x = x(x2 – 1)
⇔ x3 + 1 – 2x = x3 – x
⇔ x3 – x3 – 2x + x = -1
⇔ -x = -1
⇔ x = 1
Vậy phương trình có tập nghiệm S= { 1 }.
Bài 9: Giải các phương trình sau:
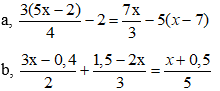
Hướng dẫn giải:

Bài 10: Giải các phương trình sau:
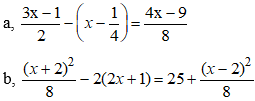
Hướng dẫn giải:


