Tìm vị trí của một điểm để tổng hai đoạn thẳng ngắn nhất

Tìm vị trí của một điểm để tổng hai đoạn thẳng ngắn nhất

Tài liệu Tìm vị trí của một điểm để tổng hai đoạn thẳng ngắn nhất Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải

1. Vẽ thêm điểm đối xứng qua trục.

2. Áp dụng tính chất hai hình đối xứng qua một trục.

3. Áp dụng bất đẳng thức trong tam giác.

B. Ví dụ minh họa

Ví dụ 1. Cho hai điểm A, B nằm trên cùng một nửa mặt phẳng bờ là đường thẳng d. Gọi B’ là điểm đối xứng của B qua đường thẳng d. Tìm trên đường thẳng d điểm M sao cho tổng MA + MB nhỏ nhất.

Giải

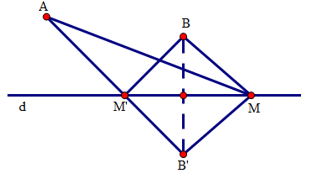
B’ là điểm đối xứng của B qua đường thẳng d, B’ cố định.

Ta có MB = MB’ (tính chất đối xứng trục).

Xét tam giác AMB’ ta có MA + MB’ ≥ AB’.

Do đó MA + MB ≥ AB’.

Dấu "=" xảy ra khi và chỉ khi A, M, B’ thẳng hàng theo thứ tự đó hay M là giao điểm của đoạn AB’ và đường thẳng d.

Vậy khi 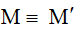là giao điểm của đoạn thẳng AB’ và đường thẳng d thì tổng MA + MB nhỏ nhất, trong đó B’ là điểm đối xứng của B qua d.

Ví dụ 2. Trên tia phân giác góc ngoài tại đỉnh C của tam giác ABC, lấy điểm M (M khác C). So sánh MA + MB và AC + BC

Giải

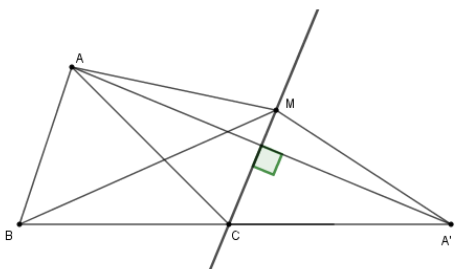
Trên tia đối của tia CB lấy điểm A’ sao cho CA = CA’.

Khi đó ta có tam giác CAA’ cân tại C có CM là phân giác 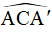nên CM cũng là đường trung trực của AA’.

Từ đó ta có: MA = MA’.

Nên MA + MB = MA’ + MB.

Xét tam giác MA’B có MA’ + MB > A’B ⇒ MA + MB > A’C + BC.

Hay MA + MB > AC + BC (vì CA = CA’).

Ví dụ 3. Cho hai điểm A, B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng d. Gọi C là điểm đối xứng với A qua d và D là giao điểm của d với đoạn thẳng BC. Vẽ điểm E bất kì trên d (E khác D). Chứng minh rằng AD + DB < AE + EB.

Giải

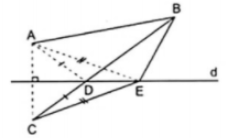
Vì C đối xứng với A qua d nên DA = DC, EA = EC. Nên

AD + DB = CD + DB = CB. (1)

AE + EB = CE + EB. (2)

Áp dụng bất đẳng thức tam giác vào tam giác BCE ta có CB < CE + EB. (3)

Từ (1), (2) và (3) suy ra AD+DB<AE+EB.

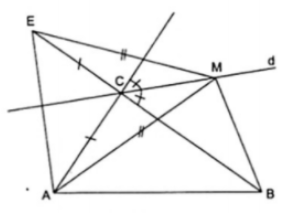
Ví dụ 4. Cho tứ giác ABCD có góc ngoài tại đỉnh C bằng góc ACB. Chứng minh rằng

AB + BD > AC + CD.

Giải

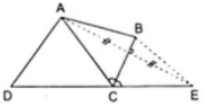
Vẽ điểm E đối xứng với điểm A qua trục BC, do C đối xứng với C qua trục BC nên 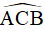đối xứng với 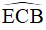qua BC suy ra 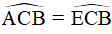hay 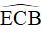là góc ngoài tại đỉnh C của tứ giác ABCD hay ba điểm D, C, E thẳng hàng.

Do đó DE = DC + CE. (1)

Vì E đối xứng với A qua BC nên

CA = CE (2)

AB = BE. (3)

Từ (1) và (2) suy ra DE = DC + AC. (*)

Từ (3) suy ra AB + BD = BD + BE. (4)

Áp dụng bất đẳng thức tam giác vào tam giác BDE ta được BD+BE >DE. (5)

Từ (4) và (5) suy ra AB + BD > DE (**)

Từ (*) và (**) suy ra AB + BD > AC + CD.

Ví dụ 5. Trên đường phân giác ngoài ở đỉnh C của tam giác ABC, lấy điểm M khác C. Chứng minh rằng AC + CB < AM + MB.

Giải

Gọi d là đường phân giác của góc ngoài tại đỉnh C.

Vẽ thêm điểm E đối xứng với điểm A qua d bằng cách, trên tia đối của tia CB lấy điểm E sao cho CE = CA ta được tam giác CAE cân tại C có d là phân giác của góc ở đỉnh nên d là đường trung trực của AE, do đó MA = ME.

Áp dụng bất đẳng thức tam giác vào tam giác MBE, ta được:

MA + MB = ME + MB > BE = CE + CB = CA + CB.

Vậy AC + CB < AM + MB.