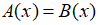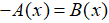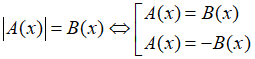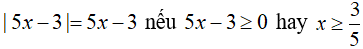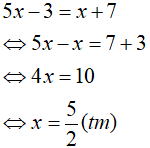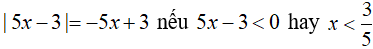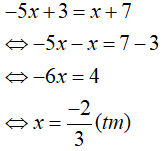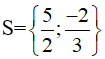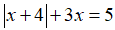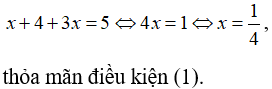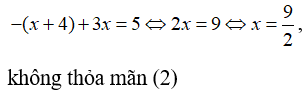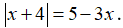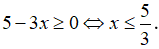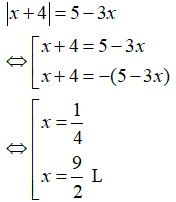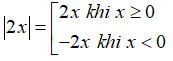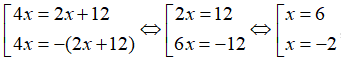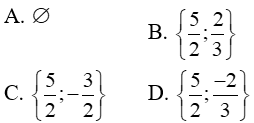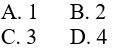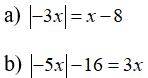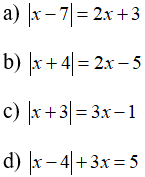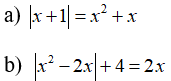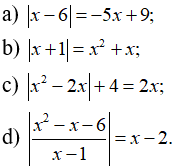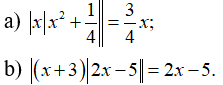Cách giải phương trình chứa dấu giá trị tuyệt đối |A(x)| = B(x)

Cách giải phương trình chứa dấu giá trị tuyệt đối |A(x)| = B(x)

Tài liệu Cách giải phương trình chứa dấu giá trị tuyệt đối |A(x)| = B(x) Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

Dạng bài: Giải phương trình |A(x)| = B(x)

A. Phương pháp giải

Để giải phương trình chứa dấu giá trị tuyệt đối |A(x)| = B(x), ta có thể lựa chọn một trong hai cách sau:

Cách 1: (Phá dấu trị tuyệt đối) Thực hiện theo các bước:

Bước 1: Đặt điều kiện để A(x) và B(x) xác định (nếu cần).

Bước 2: Xét hai trường hợp:

Trường hợp 1: Nếu 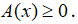. (1)

Phương trình có dạng:

=> nghiệm x và kiểm tra điều kiện (1).

Trường hợp 2: Nếu 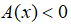(2)

Phương trình có dạng:

=> nghiệm x và kiểm tra điều kiện (2).

Bước 3: Kết luận nghiệm cho phương trình.

Cách 2: Thực hiện theo các bước:

Bước 1: Đặt điều kiện để A(x) và B(x) xác định (nếu cần) và .

Bước 2: Khi đó:

=> nghiệm x.

Bước 3: Kiểm tra điều kiện, từ đó đưa ra kết luận nghiệm cho phương trình.

B. Ví dụ minh họa

Câu 1: Tập nghiệm của phương trình 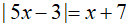là:

Lời giải:

Trường hợp 1:

Phương trình đã cho trở thành:

Trường hợp 2:

Phương trình đã cho trở thành:

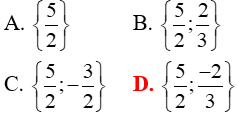
Vậy tập nghiệm của phương trình là

Câu 2: Giải phương trình:

Lời giải:

Ta có thể lựa chọn một trong hai cách sau:

Cách 1: Xét hai trường hợp:

Trường hợp 1: Nếu 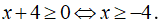(1)

Khi đó, phương trình có dạng:

Trường hợp 2: Nếu 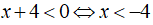(2)

Khi đó, phương trình có dạng:

Vậy, phương trình có nghiệm .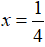

Cách 2: Viết lại phương trình dưới dạng:

Haylamdo biên soạn và sưu tầm điều kiện:

Khi đó, phương trình được biến đổi:

Vậy, phương trình có nghiệm .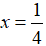

Câu 3: Giải các phương trình sau:

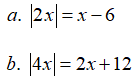
Lời giải:

a) Ta có:

Xét hai trường hợp:

Trường hợp 1: Nếu x ≥ 0 phương trình có dạng:

, không thỏa mãn điều kiện.

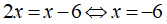
Trường hợp 2: Nếu x<0 phương trình có dạng:

, không thỏa mãn điều kiện.

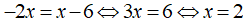
Vậy, phương trình vô nghiệm.

b) Với điều kiện:

(*)

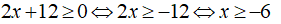
Khi đó, phương trình được biến đổi:

, thỏa mãn (*).

Vậy, phương trình có hai nghiệm x=6 và x=-2.

C. Bài tập tự luyện

Câu 1: Tập nghiệm của phương trình 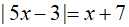là:

Caau2: Số nghiệm của phương trình 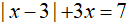là:

Câu 3: Giải các phương trình:

Câu 4: Giải các phương trình sau:

Câu 5: Giải các phương trình:

Câu 6: Giải các phương trình sau:

Câu 7: Giải các phương trình sau:

Câu 8: Giải phương trình sau bằng cách đặt ẩn phụ