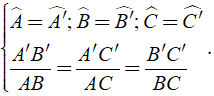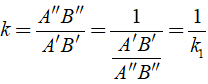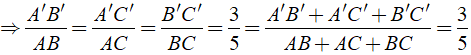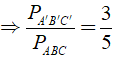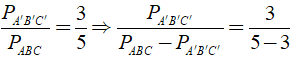Lý thuyết Khái niệm hai tam giác đồng dạng hay, chi tiết

Lý thuyết Khái niệm hai tam giác đồng dạng hay, chi tiết

Haylamdo biên soạn và sưu tầm Lý thuyết Khái niệm hai tam giác đồng dạng hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Lý thuyết

1. Tam giác đồng dạng

a) Định nghĩa

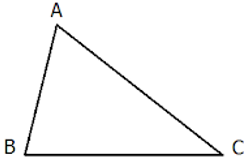
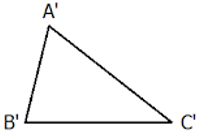
Hai tam giác được gọi là đồng dạng với nhau nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.

Tam giác ABC gọi là đồng dạng với tam giác A'B'C' nếu

Kí hiệu: Δ ABC ∼ Δ A'B'C'

Tỉ số cách cạnh tương ứng A'B'/AB = A'C'/AC = B'C'/BC = k được gọi là tỉ số đồng dạng

b) Tính chất

Hai tam giác A'B'C' và ABC đồng dạng có một số tính chất:

+ Δ ABC ∼ Δ A'B'C'

+ Nếu Δ ABC ∼ Δ A'B'C' thì Δ A'B'C' ∼ Δ ABC.

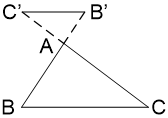
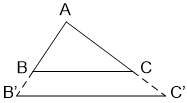
+ Nếu Δ A'B'C' ∼ Δ A''B''C'' và Δ A''B''C'' ∼ Δ ABC thì Δ ABC ∼ Δ A'B'C'

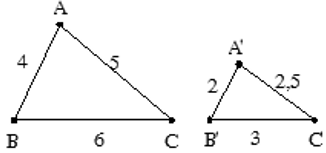
Ví dụ: Cho Δ ABC ∼ Δ A'B'C' như hình vẽ. Tính tỉ số đồng dạng ?

Hướng dẫn:

Ta có Δ ABC ∼ Δ A'B'C'. Khi đó tỉ số đồng dạng là

A'B'/AB = A'C'/AC = B'C'/BC = 2/4 = 2,5/5 = 3/6 = 1/2.

2. Định lý

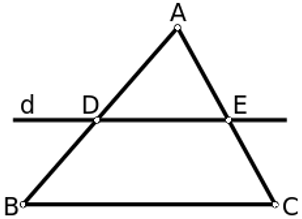
Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.

Tổng quát: Δ ABC,DE//BC ( D ∈ AB; E ∈ AC ).

Ta có: Δ ADE ∼ Δ ABC

Chú ý: Định lí cũng đúng cho trường hợp đường thẳng d cắt phần kéo dài của hai tam giác song song với cạnh còn lại.

B. Bài tập tự luyện

Bài 1: Cho Δ A'B'C' ∼ Δ A''B''C'' theo tỉ số đồng dạng k₁, Δ A''B''C'' ∼ Δ ABC theo tỉ số đồng dạng là k₂. Hỏi Δ A''B''C'' ∼ Δ A'B'C' và Δ A'B'C' ∼ Δ ABC đồng dạng theo tỉ số nào?

Hướng dẫn:

Gọi tỉ số đồng dạng của Δ A''B''C'' ∼ Δ A'B'C' là k

Ta có:

Điều đó chứng tỏ Δ A''B''C'' ∼ Δ A'B'C' theo tỉ số đồng dạng là k = 1/k₁

Gọi tỉ số đồng dạng của Δ A'B'C' ∼ Δ ABC là k₃

Thì k₁ = A'B'/A''B'', k₂ = A''B''/AB ⇒ k₃ = A'B'/AB = A'B'/A''B''.A''B''/AB = k₁.k₂

Điều đó chứng tỏ Δ A'B'C' ∼ Δ ABC theo tỉ số đồng dạng là k₃ = k₁k₂

Bài 2: Cho tam giác Δ A'B'C' ∼ Δ ABC theo tỉ số đồng dạng là k = 3/5

a) Tính tỉ số chu vi của hai tam giác đã cho.

b) Cho biết hiệu chu vi của hai tam giác trên là 40dm. Tính chu vi của hai tam giác đã cho

Hướng dẫn:

a) Ta có: Δ A'B'C' ∼ Δ ABC

b) Theo giả thiết ta có: P_ABC - P_A'B'C' = 40dm

Khi đó ta có:

hay P_A'B'C'/40 = 3/2 ⇒ P_A'B'C' = 60( dm ); P_ABC = 20dm.