Tìm điều kiện của hình A để hình B trở thành hình vuông

Tìm điều kiện của hình A để hình B trở thành hình vuông

Tài liệu Tìm điều kiện của hình A để hình B trở thành hình vuông Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải

1. Sử dụng định nghĩa và các tính chất của hình vuông

• Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.
• Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.
• Đường chéo của hình vuông vừa bằng nhau vừa vuông góc với nhau.

2. Nếu bài toán chỉ yêu cầu tìm vị trí của một điểm nào đó để một hình trở thành hình vuông ta làm như sau: Giả sử hình đó là hình vuông rồi dựa vào các tính chất của hình vuông để chỉ ra vị trí cần tìm.

B. Ví dụ minh họa

Ví dụ 1. Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để hình bình hành EFGH là hình vuông.

Giải

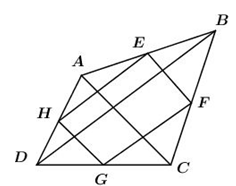
Ta có EH, GF lần lượt là đường trung bình của tam giác ABD, BCD nên

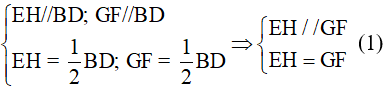
Suy ra EFGH là hình bình hành.

Hình bình hành EFGH là hình vuông khi và chỉ khi

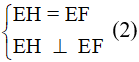
Mặt khác EF, GH lần lượt là đường trung bình của tam giác ABC, ACD nên

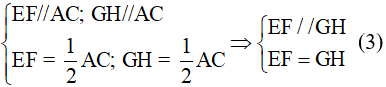
Từ (1), (2) và (3)

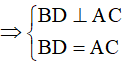
thì hình bình hành EFGH là hình vuông.

Ví dụ 2. Cho hình vuông ABCD. M là điểm nằm trong hình vuông. Gọi E, F lần lượt là hình chiếu của M trên cạnh AD và AB. Tứ giác AEMF là hình vuông khi?

Giải

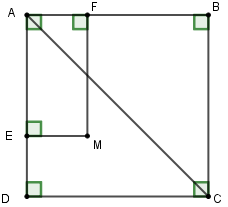
Tứ giác AFME có: 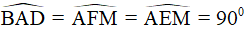nên AEMF là hình chữ nhật.

Để hình chữ nhật AEMF là hình vuông thì AM là phân giác .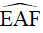

Mà ta lại có: AC là phân giác 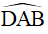(do ABCD là hình vuông).

Nên suy ra .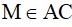

Ví dụ 3. Cho tam giác ABC vuông tại A. Gọi M, N, P lần lượt là các trung điểm của AB, BC, AC. Tam giác ABC cần có thêm điều kiện gì để hình chữ nhật AMNP là hình vuông?

Giải

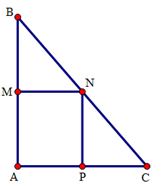
Ta có MN, NP là hai đường trung bình của tam giác ABC

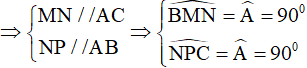
(các góc ở vị trí đồng vị)

Vậy tứ giác MNPA có 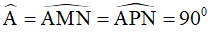nên là hình chữ nhật.

Hình chữ nhật AMNP là hình vuông ⇔ AM = AP.

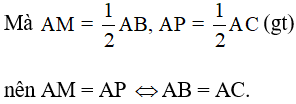
Vậy nếu tam giác ABC vuông cân tại A thì hình chữ nhật AMNP là hình vuông.

Ví dụ 4. Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC. Chúng cắt các cạnh AC và AB thứ tự ở E và F.

a) Tứ giác AEDF là hình gì? Vì sao?

b) Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi?

c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình vuông?

Giải

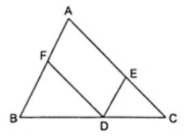
a) Tứ giác AEDF là hình bình hành.

Giải thích: Từ giả thiết

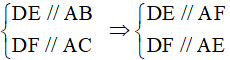
Tứ giác AEDF có các cạnh đối song song nên nó là là hình bình hành.

b) Giả sử AEDF là hình thoi khi đó theo tính chất về đường chéo của hình thoi thì AD là đường phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì tứ giác AEDF là hình thoi.

c) Nếu tam giác ABC vuông tại A thì hình bình hành AEDF là hình chữ nhật. Nếu tam giác ABC vuông tại A và D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF vừa là hình chữ nhật vừa là hình thoi nên nó là hình vuông.

Ví dụ 5. Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD và DA. Hai đường chéo AC và BD phải thoả mãn những điểu kiện nào để M, N, P, Q là bốn đỉnh của

a) Hình chữ nhật?

b) Hình thoi?

c) Hình vuông?

Giải

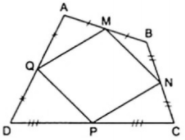
Trước hết ta chứng minh tứ giác MNPQ là hình bình hành.

Ta có MN, PQ lần lượt là đường trung bình của tam giác ABC và ACD

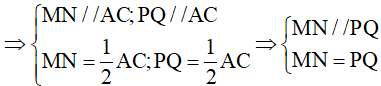
Suy ra tứ giác MNPQ là hình bình hành.

a) MNPQ là hình chữ nhật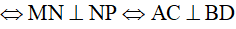(vì MN//AC và PN//BD)

Điều kiện cần tìm là hai đường chéo AC, BD vuông góc với nhau.

b) MNPQ là hình thoi

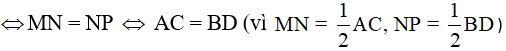
Điều kiện cần tìm là các đường chéo AC và BD bằng nhau.

c) MNPQ là hình vuông

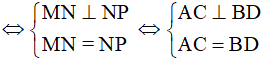
Điều kiện cần tìm là các đường chéo AC, BD bằng nhau và vuông góc với nhau.