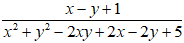Cách chứng minh phân thức luôn có nghĩa cực hay, có đáp án
Cách chứng minh phân thức luôn có nghĩa cực hay, có đáp án
Tài liệu Cách chứng minh phân thức luôn có nghĩa cực hay, có đáp án Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.
A. Phương pháp giải
Vận dụng các phép biến đổi toán học để chứng minh mẫu thức luôn khác 0
B. Ví dụ minh họa
Ví dụ 1: Chứng minh các phân thức sau luôn có nghĩa
Hướng dẫn giải:
a, Ta có: x2 ≥ 0 với mọi x ⇒ x2 + 1≥ 1 với mọi x
Do đó x2 + 1 ≠ 0 với mọi x
Vậy phân thức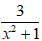 
luôn có nghĩa với mọi x
b, Ta có (x – 1)2 ≥ 0 với mọi x ⇒ (x – 1)2 + 2 ≥ 2 với mọi x
Do đó: (x – 1)2 + 2 ≠ 0 với mọi x
Vậy phân thức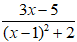 
luôn có nghĩa với mọi x
Ví dụ 2: Chứng minh các phân thức sau luôn có nghĩa
Hướng dẫn giải:
a, Ta có (x – 1)2 ≥ 0 với mọi x ⇒ (x – 1)2 + 1 ≥ 1 với mọi x
Do đó: (x – 1)2 + 1 ≠ 0 với mọi x
Vậy phân thức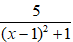 
luôn có nghĩa với mọi x
b, Ta có x2 + 4x + 7 = x2 + 4x + 4 + 3 = (x + 2)2 + 3
Vì (x + 2)2 ≥ 0 với mọi x ⇒ (x + 2)2 + 3 ≥ 3 với mọi x
Vậy phân thức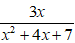 
luôn có nghĩa với mọi x
Ví dụ 3: Chứng minh các phân thức sau luôn xác định.
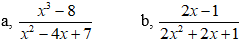
Hướng dẫn giải:
a, Ta có x2 - 4x + 7 = x2 – 4x + 4 + 3 = (x - 2)2 + 3
Mà (x – 2)2 ≥ 0 với mọi x ⇒ (x – 2)2 + 3 ≥ 3 với mọi x
Do đó (x – 2)2 + 3 ≠ 0 với mọi x
Vậy phân thức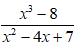 
luôn xác định với mọi x
b, Ta có: 2x2 + 2x + 1 = x2 + x2 + 2x + 1 = x2 + (x + 1)2 > 0 với mọi x
Do đó phân thức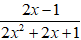 
luôn xác định với mọi x
C. Bài tập vận dụng
Bài 1: Trong các phân thức sau, phân thức nào luôn có nghĩa
Đáp án: B
Phân thức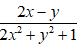 
luôn có nghĩa vì x2 ≥ 0 với ∀ x; y2 ≥ 0 với ∀y
⇒ mẫu thức 2x2 + y2 + 1 ≥ 1 với mọi x,y.
Do đó mẫu thức 2x2 + y2 + 1 ≠ 0 với mọi x,y
Vậy phân thức 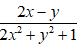luôn có nghĩa với mọi x
Bài 2: Trong các phân thức sau, phân thức nào luôn có nghĩa với mọi x
Đáp án: A
Phân thức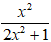 
luôn có nghĩa vì x2 ≥ 0 với ∀ x ⇒ mẫu thức 2x2 + 1 ≥ 1 với mọi x
Do đó mẫu thức 2x2 + 1 ≠ 0 với mọi x
Vậy phân thức 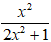luôn có nghĩa với mọi x
Bài 3: Với x ≠ 0, x ≠ 1 phân thức nào sau đây luôn được xác định.
Đáp án: C
Phân thức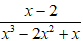 
luôn có nghĩa với x ≠ 0, x ≠ 1
Vì mẫu thức x3 - 2x2 + x = x(x2 - 2x + 1) = x (x - 1)2 ≠ 0 với mọi x ≠ 0, x ≠ 1
Vậy phân thức 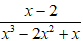luôn có nghĩa với mọi x.
Bài 4: Trong các phân thức sau, phân thức nào luôn có nghĩa với mọi x
Đáp án: D
Ta có –x2 + 2x – 2 = -(x2 - 2x + 1) – 1 = -(x - 1)2 – 1 < 0 với mọi x.
Do đó mẫu thức –x2 + 2x – 2 ≠ 0 với mọi x
Vậy phân thức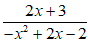 
luôn có nghĩa với mọi x
Bài 5: Với x ≠ -1, x ≠ 1, phân thức nào sau đây luôn được xác định
Đáp án: A
Haylamdo biên soạn và sưu tầm x ≠ -1, x ≠ 1 ta có x2 – 1 ≠ 0 .
Vậy phân thức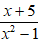 
luôn có nghĩa với mọi x ≠ -1, x ≠ 1
Bài 6: Chứng minh các phân thức sau luôn có nghĩa.
Hướng dẫn giải:
a, Ta có: x2 + 2x + 4 = x2 + 2x + 1 + 3 = (x + 1)2 + 3 ≥ 3 với mọi x
Do đó mẫu thức x2 + 2x +4 ≠ 0 với mọi x
Vậy phân thức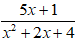 
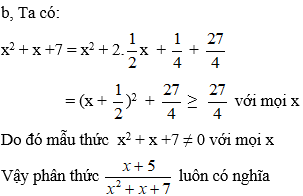
luôn có nghĩa
Bài 7: Chứng minh các phân thức sau luôn có nghĩa.
Hướng dẫn giải:
a, Ta có -x2 + 4x – 5 = -( x2 - 4x + 4) – 1 = -(x - 2)2 – 1 ≤ -1 với mọi x
Do đó mẫu thức -x2 + 4x – 5 ≠ 0 với mọi x
Vậy phân thức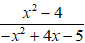 
luôn có nghĩa
b, Ta có 2x2 - 4x + 3 = 2( x2 - 2x + 1) + 1 = 2(x - 1)2 + 1 ≥ 1 với mọi x
Do đó mẫu thức 2x2 - 4x + 3 ≠ 0 với mọi x
Vậy phân thức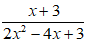 
luôn có nghĩa
Bài 8: Chứng minh các phân thức sau luôn xác định với mọi x
Hướng dẫn giải:
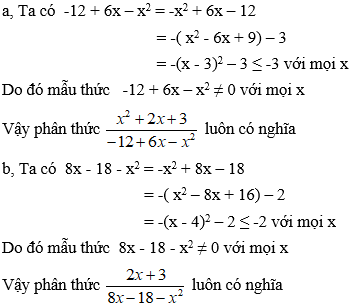
Bài 9: Chứng minh các phân thức sau luôn có nghĩa.
Hướng dẫn giải:
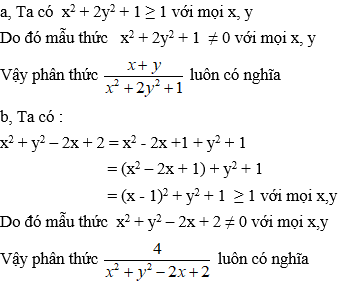
Bài 10: Chứng minh các phân thức sau luôn có nghĩa.
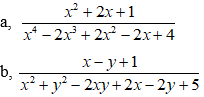
Hướng dẫn giải:
a, Ta có:
x4 - 2x3 + 2x2 - 2x + 4
= (x4 - 2x3 + x2) + (x2 - 2x + 1) + 3
= x2(x2 – 2x + 1) + (x2 – 2x + 1) + 3
= (x2 – 2x + 1) (x2 + 1) + 3
= ( x - 1)2(x2 + 1) + 3
Vì ( x - 1)2(x2 + 1) ≥ 0 với mọi x ⇒ ( x - 1)2(x2 + 1) + 3 ≥ 3 với mọi x
Do đó mẫu thức x4 - 2x3 + 2x2 - 2x +4 =( x - 1)2(x2 + 1) + 3 ≠ 0 với mọi x
Vậy phân thức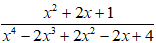 
luôn có nghĩa
b, Ta có:
x2 + y2 - 2xy + 2x - 2y + 5
= (x2 + y2 + 1- 2xy + 2x - 2y) + 4
= (x - y + 1)2 + 4
Vì (x- y + 1)2 ≥ 0 với mọi x,y nên (x - y + 1)2 + 4 ≠ 0 với mọi x,y
Vậy phân thức 
luôn xác định với mọi giá trị x,y
