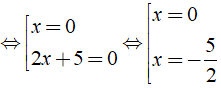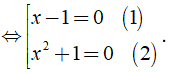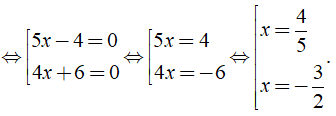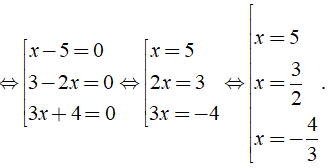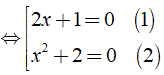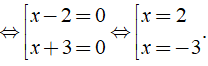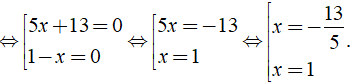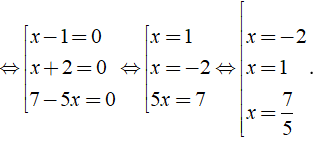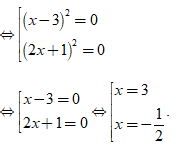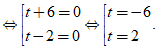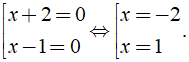Lý thuyết Phương trình tích hay, chi tiết
Lý thuyết Phương trình tích hay, chi tiết
Haylamdo biên soạn và sưu tầm Lý thuyết Phương trình tích hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.
A. Lý thuyết
1. Phương trình tích và cách giải
Phương trình tích có dạng A( x ).B( x ) = 0
Cách giải phương trình tích A( x ).B( x ) = 0 ⇔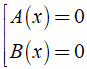 
Cách bước giải phương trình tích
Bước 1: Đưa phương trình đã cho về dạng tổng quát A( x ).B( x ) = 0 bằng cách:
Chuyển tất cả các hạng tử của phương trình về vế trái. Khi đó vế phải bằng 0.
Phân tích đa thức ở vế phải thành nhân tử
Bước 2: Giải phương trình và kết luận
Ví dụ 1: Giải phương trình ( x + 1 )( x + 4 ) = ( 2 - x )( 2 + x )
Hướng dẫn:
Ta có: ( x + 1 )( x + 4 ) = ( 2 - x )( 2 + x ) ⇔ x2 + 5x + 4 = 4 - x2
⇔ 2x2 + 5x = 0 ⇔ x( 2x + 5 ) = 0
Vậy phương trình đã cho có tập nghiệm là S = { - 5/2; 0 }
Ví dụ 2: Giải phương trình x3 - x2 = 1 - x
Hướng dẫn:
Ta có: x3 - x2 = 1 - x ⇔ x2( x - 1 ) = - ( x - 1 )
⇔ x2( x - 1 ) + ( x - 1 ) = 0 ⇔ ( x - 1 )( x2 + 1 ) = 0
( 1 ) ⇔ x - 1 = 0 ⇔ x = 1.
( 2 ) ⇔ x2 + 1 = 0 (Vô nghiệm vì x2 ≥ 0 ⇒ x2 + 1 ≥ 1 )
Vậy phương trình đã cho có tập nghiệm là S = { 1 }.
B. Bài tập tự luyện
Bài 1: Giải các phương trình sau:
a) ( 5x - 4 )( 4x + 6 ) = 0
b) ( x - 5 )( 3 - 2x )( 3x + 4 ) = 0
c) ( 2x + 1 )( x2 + 2 ) = 0
d) ( x - 2 )( 3x + 5 ) = ( 2x - 4 )( x + 1 )
Hướng dẫn:
a) Ta có: ( 5x - 4 )( 4x + 6 ) = 0
Vậy phương trình đã cho có tập nghiệm là S = { - 3/2; 4/5 }.
b) Ta có: ( x - 5 )( 3 - 2x )( 3x + 4 ) = 0
Vậy phương trình đã cho có tập nghiệm là S = { - 4/3; 3/2; 5 }.
c) Ta có: ( 2x + 1 )( x2 + 2 ) = 0
Giải ( 1 ) ⇔ 2x + 1 = 0 ⇔ 2x = - 1 ⇔ x = - 1/2.
Ta có: x2 ≥ 0 ⇒ x2 + 2 ≥ 2 ∀ x ∈ R
⇒ Phương trình ( 2 ) vô nghiệm.
Vậy phương trình đã cho có tập nghiệm S = { - 1/2 }.
d) Ta có: ( x - 2 )( 3x + 5 ) = ( 2x - 4 )( x + 1 )
⇔ ( x - 2 )( 3x + 5 ) - 2( x - 2 )( x + 1 ) = 0
⇔ ( x - 2 )[ ( 3x + 5 ) - 2( x + 1 ) ] = 0
⇔ ( x - 2 )( x + 3 ) = 0
Vậy phương trình đã cho có tập nghiệm là S = { - 3;2 }.
Bài 2: Giải các phương trình sau:
a) ( 2x + 7 )2 = 9( x + 2 )2
b) ( x2 - 1 )( x + 2 )( x - 3 ) = ( x - 1 )( x2 - 4 )( x + 5 )
c) ( 5x2 - 2x + 10 )2 = ( 3x2 + 10x - 8 )2
d) ( x2 + x )2 + 4( x2 + x ) - 12 = 0
Hướng dẫn:
a) Ta có: ( 2x + 7 )2 = 9( x + 2 )2
⇔ ( 2x + 7 )2 - 9( x + 2 )2 = 0
⇔ [ ( 2x + 7 ) + 3( x + 2 ) ][ ( 2x + 7 ) - 3( x + 2 ) ] = 0
⇔ ( 5x + 13 )( 1 - x ) = 0
Vậy phương trình đã cho có tập nghiệm là S = { - 13/5; 1 }.
b) Ta có: ( x2 - 1 )( x + 2 )( x - 3 ) = ( x - 1 )( x2 - 4 )( x + 5 )
⇔ ( x2 - 1 )( x + 2 )( x - 3 ) - ( x - 1 )( x2 - 4 )( x + 5 ) = 0
⇔ ( x - 1 )( x + 1 )( x + 2 )( x - 3 ) - ( x - 1 )( x - 2 )( x + 2 )( x + 5 ) = 0
⇔ ( x - 1 )( x + 2 )[ ( x + 1 )( x - 3 ) - ( x - 2 )( x + 5 ) ] = 0
⇔ ( x - 1 )( x + 2 )[ ( x2 - 2x - 3 ) - ( x2 + 3x - 10 ) ] = 0
⇔ ( x - 1 )( x + 2 )( 7 - 5x ) = 0
Vậy phương trình có tập nghiệm là S = { - 2; 1; 7/5 }.
c) Ta có: ( 5x2 - 2x + 10 )2 = ( 3x2 + 10x - 8 )2
⇔ ( 5x2 - 2x + 10 )2 - ( 3x2 + 10x - 8 )2 = 0
⇔ [ ( 5x2 - 2x + 10 ) - ( 3x2 + 10x - 8 ) ][ ( 5x2 - 2x + 10 ) + ( 3x2 + 10x - 8 ) ] = 0
⇔ ( 2x2 - 12x + 18 )( 8x2 + 8x + 2 ) = 0
⇔ 4( x2 - 6x + 9 )( 4x2 + 4x + 1 ) = 0
⇔ 4( x - 3 )2( 2x + 1 )2 = 0
Vậy phương trình đã cho có tập nghiệm S = {- 1/2; 3}.
d) Ta có: ( x2 + x )2 + 4( x2 + x ) - 12 = 0
Đặt t = x2 + x, khi đó phương trình trở thành:
t2 + 4t - 12 = 0 ⇔ ( t + 6 )( t - 2 ) = 0
+ Với t = - 6, ta có: x2 + x = - 6 ⇔ x2 + x + 6 = 0 ⇔ ( x + 1/2 )2 + 23/4 = 0
Mà ( x + 1/2 )2 + 23/4 ≥ 23/4 ∀ x ∈ R ⇒ Phương trình đó vô nghiệm.
+ Với t = 2, ta có x2 + x = 2 ⇔ x2 + x - 2 = 0
⇔ ( x + 2 )( x - 1 ) = 0 ⇔ 
Vậy phương trình có tập nghiệm là S = { - 2;1 }.
