Chứng minh hai đoạn thẳng, hai góc bằng nhau trong hình thoi
Chứng minh hai đoạn thẳng, hai góc bằng nhau trong hình thoi
Tài liệu Chứng minh hai đoạn thẳng, hai góc bằng nhau trong hình thoi Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải
1. Sử dụng định nghĩa hình thoi
Hình thoi là tứ giác có bốn cạnh bằng nhau.
Tứ giác ABCD là hình thoi ⇔ AB = BC = CD = DA.
2. Áp dụng các tính chất của hình thoi.
Hình thoi có tất cả các tính chất của hình bình hành. Nhưng cần chú ý các tính chất về đường chéo. Trong hình thoi:
a) Hai đường chéo vuông góc với nhau.
b) Hai đường chéo là các đường phân giác của các góc của hình thoi.
3. Xác định tam giác vuông chứa đoạn cần tính để áp dụng định lí Py-ta-go.
B. Ví dụ minh họa
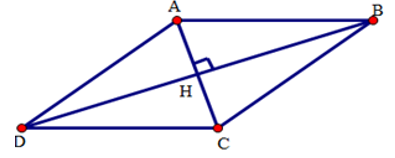
Ví dụ 1. Hai đường chéo của một hình thoi bằng 8cm và 10cm. Hỏi cạnh của hình thoi bằng bao nhiêu?
Giải
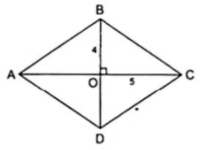
Xét hình thoi ABCD có O là giao điểm của hai đường chéo và AC = 10cm, BD = 8cm. Vì hình thoi có tất cả các cạnh bằng nhau nên ta chỉ cần tính một cạnh, chẳng hạn cạnh BC. Áp dụng tính chất về đường chéo và giả thiết vào hình thoi ABCD, ta được
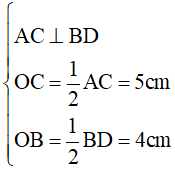
⇒ΔBOC vuông tại O và có hai cạnh góc vuông là 4cm và 5cm.
Áp dụng định lí Py-ta-go vào tam giác vuông BOC, ta được
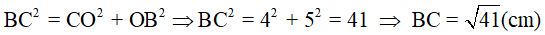
Vậy cạnh của hình thoi là 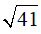 cm.
cm.
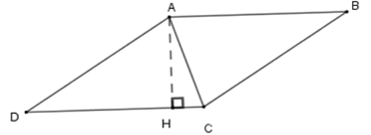
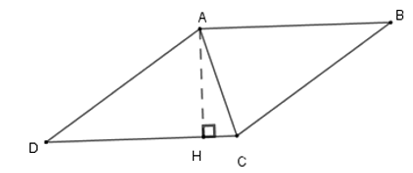
Ví dụ 2. Cho hình thoi ABCD có góc A tù. Biết đường cao kẻ từ đỉnh A đến cạnh CD chia đôi cạnh đó. Tính các góc của hình thoi.
Giải
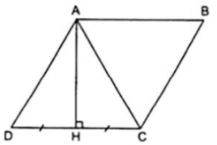
Gọi H là chân đường cao kẻ từ A đến cạnh CD và từ giả thiết, ta có:
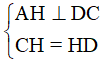
⇒AH là đường trung trực của đoạn CD nên AC = AD (1)
Áp dụng định nghĩa vào hình thoi ABCD, ta được AD = CD (2)
Từ (1) và (2) suy ra AC = CD = DA nên tam giác ACD là tam giác đều, do đó 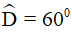
Vì góc D và góc BAD là hai góc trong cùng phía của AB//CD nên chúng bù nhau hay
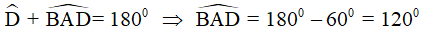
Áp dụng tính chất về góc vào hình thoi ta được
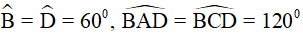
Ví dụ 3. Chứng minh rằng các đường cao của hình thoi bằng nhau.
Giải
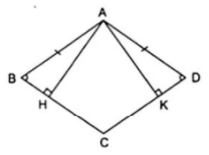
Xét hình thoi ABCD, kẻ hai đường cao 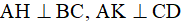 .
.
Ta phải chứng minh AH = AK.
Áp dụng định nghĩa, tính chất về góc và giả thiết vào hình thoi ABCD, ta được:
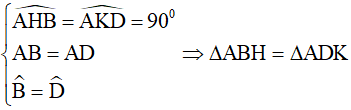
(trường hợp cạnh huyền, góc nhọn).
Suy ra AH = AK.
C. Bài tập vận dụng
Câu 1. Hình thoi có chu vi bằng 20cm thì độ dài cạnh của nó bằng
A. 4cm.
B. 5cm.
C. 8cm.
D. Cả A, B, C đều sai.
Câu 2. Hình thoi có chu vi bằng 36cm thì độ dài cạnh của nó bằng.
A. 12 cm.
B. 4 cm.
C. 9 cm.
D. Đáp án khác.
Câu 3. Cho hình thoi ABCD có chu vi bằng 16cm, đường cao AH bằng 2cm. Tính các góc của hình thoi. Hãy chọn câu đúng.
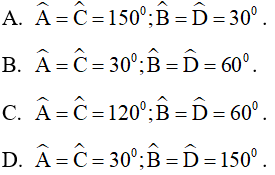
Câu 4. Cho hình thoi ABCD có chu vi bằng 24cm, đường cao AH bằng 3cm. Tính 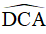 .
.
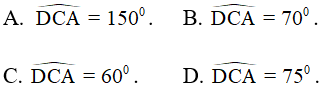
Câu 5. Cho hình thoi có độ dài hai đường chéo là 24cm và 10cm. Tính độ dài cạnh hình thoi.
A. 12cm.
B. 13cm.
C. 14cm.
D. 15cm.
Câu 6. Cho hình thoi có độ dài hai đường chéo là 12cm và 16cm. Tính độ dài cạnh hình thoi.
A. 12 cm.
B. 8 cm.
C. 20 cm.
D. 10 cm.
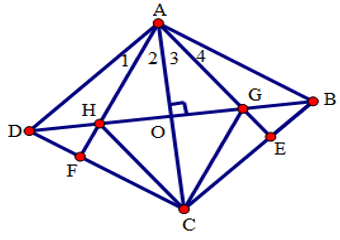
Câu 7. Cho hình thoi ABCD. Trên các cạnh BC và CD lần lượt lấy hai điểm E và F sao cho BE = DF. Gọi G, H thứ tự là giao điểm của AE, AF với đường chéo BD. Cho OC = 4; OH = 3 với O là giao điểm hai đường chéo AC và BD. Tính chu vi tứ giác AHCG.
A. 20 cm.
B. 24 cm.
C. 16 cm.
D. 8 cm.
Câu 8. Cho tứ giác ABCD có 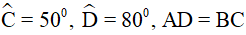 . Gọi E, F lần lượt là trung điểm của các cạnh AB và CD. Tính số đo góc EFC.
. Gọi E, F lần lượt là trung điểm của các cạnh AB và CD. Tính số đo góc EFC.
A. 750 .
B. 950 .
C. 1050 .
D. 1200 .
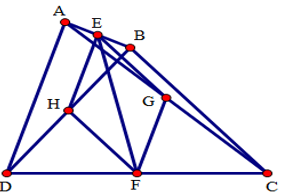
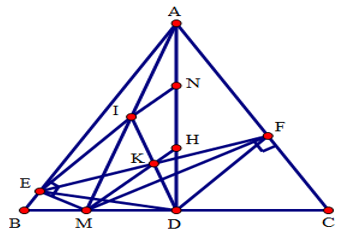
Câu 9. Cho tam giác ABC đều, H là trực tâm, đường cao AD. M là điểm bất kì trên trên cạnh BC. Gọi E, F lần lượt là hình chiếu của M trên AB, AC, gọi I là trung điểm của đoạn thẳng AM, ID cắt EF tại K.
Chọn câu sai.
A. M, H, K thẳng hàng.
B. ΔIED đều.
C. Tứ giác EIFD là hình thoi.
D. ID>IF.

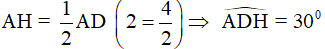
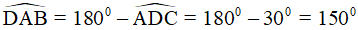
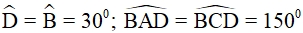
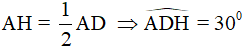
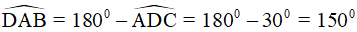
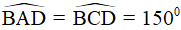
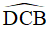 (tính chất hình thoi) nên
(tính chất hình thoi) nên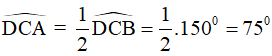
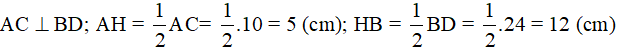
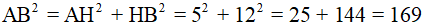
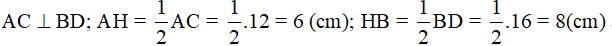
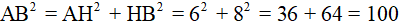
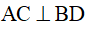 (do O là giao điểm của hai đường chéo của hình thoi)
(do O là giao điểm của hai đường chéo của hình thoi)
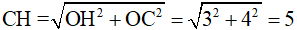
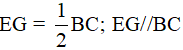
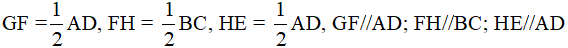
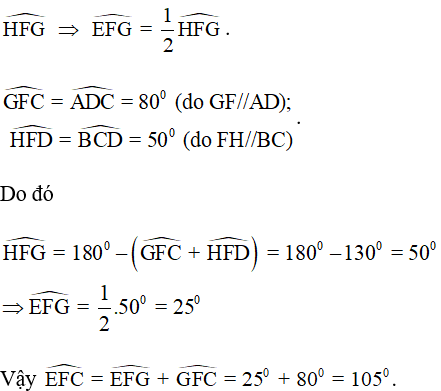
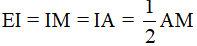
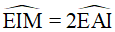
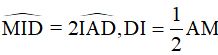
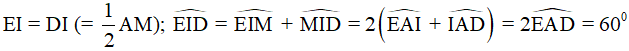
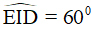 nên là tam giác đều, từ đó EI = ED = ID.
nên là tam giác đều, từ đó EI = ED = ID.