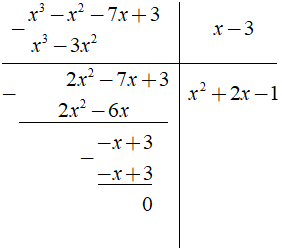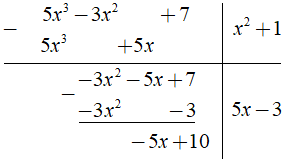Lý thuyết Chia đa thức một biến đã sắp xếp hay, chi tiết

Lý thuyết Chia đa thức một biến đã sắp xếp hay, chi tiết

Haylamdo biên soạn và sưu tầm Lý thuyết Chia đa thức một biến đã sắp xếp hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Lý thuyết

1. Phương pháp

Ta trình bày phép chia tương tự như cách chia các số tự nhiên. Với hai đa thức A và B của một biến, B≠0 tồn tại duy nhất hai đa thức Q và R sao cho:

A = B.Q + R, với R=0 hoặc bậc của R nhỏ hơn bậc của B.

   Nếu R=0, ta được phép chia hết.

   Nếu R≠0, ta được phép chia có dư.

Ví dụ: Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi làm phép chia:

a, ( x³ - 7x + 3 - x² ):( x - 3 ).

b, ( 5x³ + 7 - 3x² ):( x² + 1 ).

Hướng dẫn:

a) Ta có:

Khi đó ta có: ( x³ - 7x + 3 - x² ) = ( x - 3 ).( x² + 2x - 1 )

b) Ta có

Khi đó ta có ( 5x³ + 7 - 3x² ) = ( x² + 1 )( 5x - 3 ) - 5x + 10.

B. Bài tập tự luyện

Bài 1: Thực hiện các phép chia

a, ( 2x³ - 26x - 24 ):( x² + 4x + 3 )

b, ( x³ - 9x² + 28x - 30 ):( x - 3 )

Hướng dẫn:

a) Ta có phép chia

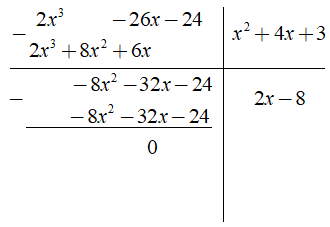
Vậy ( 2x³ - 26x - 24 ) = ( x² + 4x + 3 )( 2x - 8 )

b) Ta có phép chia

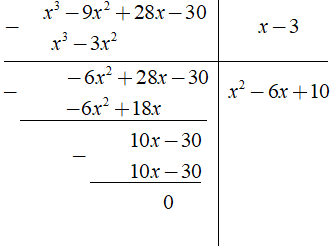
Vậy ( x³ - 9x² + 28x - 30 ) = ( x - 3 )( x² - 6x + 10 )

Bài 2: Tính nhanh các phép chia sau:

a, ( x⁶ + 2x³y² + y⁴ ):( x³ + y² )

b, ( 625x⁴ - 1 ):[ ( 5x + 1 )( 5x - 1 ) ]

Hướng dẫn:

a) Ta có ( x⁶ + 2x³y² + y⁴ ):( x³ + y² ) = ( x³ + y² )²:( x³ + y² ) = ( x³ + y² )

Vậy ( x⁶ + 2x³y² + y⁴ ):( x³ + y² ) = ( x³ + y² )

b) Ta có ( 625x⁴ - 1 ):[ ( 5x + 1 )( 5x - 1 ) ] = [ ( 25x² - 1 )( 25x² + 1 ) ]:( 25x² - 1 ) = ( 25x² + 1 )

Vậy ( 625x⁴ - 1 ):[ ( 5x + 1 )( 5x - 1 ) ] = ( 25x² + 1 )

Bài 3: Tìm các số nguyên n để giá trị của biểu thức n³ + 6n² -7n + 4 chia hết cho giá trị của biểu thức n - 2.

Hướng dẫn:

Ở đây, ta có thực hiện đặt phép chia như câu 1 để tìm số dư và tìm điều kiện giá trị của n để thỏa mãn đề bài. Nhưng bài này ta làm cách biến đổi như sau:

Ta có n³ + 6n² -7n + 4 = ( n³ - 3n².2 + 3.n.2² - 8 ) + 12n² - 19n + 12

= ( n - 2 )³ + 12n( n - 2 ) + 5( n - 2 ) + 22

Khi đó ta có: (n³ + 6n² - 7n + 4)/(n - 2) = ( n - 2 )² + 12n + 5 + 22/(n - 2)

Để giá trị của biểu thức n³ + 6n² -7n + 4 chia hết cho giá trị của biểu thức n - 2.

⇔ ( n - 2 ) ∈ UCLN( 22 ) = {± 1; ± 2; ± 11; ± 22 }

⇒ n ∈ {- 20; - 9; 0; 1; 3; 4; 13; 24 }

Vậy các giá trị nguyên của n cần tìm là n ∈ { - 20; - 9; 0; 1; 3; 4; 13; 24 }