Cách phân tích đa thức thành nhân tử bằng phương pháp đổi biến số, đặt ẩn phụ
Cách phân tích đa thức thành nhân tử bằng phương pháp đổi biến số, đặt ẩn phụ
Tài liệu Cách phân tích đa thức thành nhân tử bằng phương pháp đổi biến số, đặt ẩn phụ Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải
+ Bước 1. Đặt t = f(x) , đưa đa thức đã cho về đa thức biến t.
+ Bước 2. Phân tích đa thức ẩn t đó thành nhân tử bằng các phương pháp: Dùng hằng đẳng thức, nhóm hạng tử, tách ( thêm, bớt) hạng tử.
+ Bước 3. Sau khi phân tích đa thức thành nhân tử theo ẩn t, ta trả lại theo biến x.
B. Ví dụ minh họa
Câu 1. Phân tích đa thức 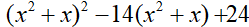
A. (x+ 2). (x- 1). (x+ 4).( x- 3)
B. ( x + 2). (x+ 1). ( x- 3). (x – 4)
C. (x – 2). (x- 1). (x- 4). (x+3)
D. Đáp án khác
Lời giải
Đặt t = x2 + x, ta có:
(x2 + x)2 - 14(x2 + x) + 24 = t2 - 14t + 24
+ Ta có:
t2 - 14t + 24 = t2 - 2t - 12t + 24
= (t2 - 2t) - (12t - 24)
= t(t - 2) - 12(t - 2) = (t - 2).(t - 12)
+ Do đó,
(x2 + x)2 - 14(x2 + x) + 24 = (x2 + x - 2).(x2 + x - 12)
= [(x2 - x) + (2x - 2)].[(x2 - 16) + (x + 4)]
= [x(x - 1) + 2(x - 1)].[(x + 4).(x - 4) + 1.(x + 4)]
= (x + 2).(x - 1).(x + 4).(x + 3)
Chọn A.
Ví dụ 2. Phân tích các đa thức (x2 + x)2 + 4x2 + 4x - 12 thành nhân tử
A. (x + 1).(x - 2).(x2 + x + 6)
B. (x - 1).(x - 2).(x2 + x + 6)
C. (x - 1).(x + 2).(x2 + x + 6)
D. Đáp án khác
Lời giải
+ Ta có: (x2 + x)2 + 4x2 + 4x - 12 = (x2 + x)2 + 4(x2 + x) - 12
Đặt t = x2 + x, khi đó:
(x2 + x)2 + 4(x2 + x) - 12 = t2 + 4t - 12 (1)
+ Ta có:
t2 + 4t - 12 = t2 - 4 + 4t - 8
= (t + 2).(t - 2) + 4(t - 2)
= (t - 2).(t + 2 + 4) = (t - 2).(t + 6) (2)
+ Từ (1) và (2) suy ra:
(x2 + x)2 + 4x2 + 4x - 12
= (x2 + x - 2).(x2 + x + 6)
= [(x2 - 1) + (x - 1)].(x2 + x + 6)
= [(x - 1).(x + 1) + (x - 1)].(x2 + x + 6)
= (x - 1).(x + 1 + 1).(x2 + x + 6) = (x - 1).(x + 2).(x2 + x + 6)
Chọn C.
Ví dụ 3. Phân tích đa thức (x2 + x + 1).(x2 + x + 2) - 12 thành nhân tử
A. (x + 1).(x + 2).(x2 - x + 5)
B. (x - 1).(x + 2).(x2 + x + 5)
C. (x - 1).(x - 2).(x2 + x + 5)
D. Đáp án khác
Lời giải
Đặt t = x2 + x + 1 => t + 1 = x2 + x + 2
Khi đó: (x2 + x + 1).(x2 + x + 2) - 12 = t.(t + 1) - 12 (1)
Ta có:
t(t + 1) - 12 = t2 + t - 12
= (t2 - 9) + (t - 3)
= (t + 3).(t - 3) + 1.(t - 3)
= (t - 3).(t + 3 + 1) = (t - 3).(t + 4) (2)
Từ (1) và (2) suy ra:
(x2 + x + 1).(x2 + x + 2) - 12 = (x2 + x + 1 - 3).(x2 + x + 1 + 4)
= (x2 + x - 2).(x2 + x + 5) = [(x2 - 1) + (x - 1)].(x2 + x + 5)
= [(x + 1).(x - 1) + (x - 1)].(x2 + x + 5)
= (x - 1).(x + 2).(x2 + x + 5)
Chọn B.
C. Bài tập trắc nghiệm
Câu 1. Phân tích đa thức (x2 + 4x + 8)2 + 3x(x2 + 4x + 8) + 2x2 thành nhân tử
A. (x - 2).(x + 4).(x2 + 5x + 8)
B. (x + 2).(x - 4).(x2 + 5x + 8)
C. (x - 2).(x - 4).(x2 + 5x + 8)
D. (x + 2).(x + 4).(x2 + 5x + 8)
+ Đặt t = x2 + 4x + 8, khi đó:
(x2 + 4x + 8)2 + 3x(x2 + 4x + 8) + 2x2 = t2 + 3xt + 2x2
+ Ta có:
t2 + 3xt + 2x2 = (t2 + xt) + (2xt + 2x2)
= t.(t + x) + 2x.(t + x) = (t + 2x).(t + x)
Do đó: (x2 + 4x + 8)2 + 3x(x2 + 4x + 8x) + 2x2
= (x2 + 4x + 8 + 2x).(x2 + 4x + 8 + x)
= (x2 + 6x + 8).(x2 + 5x + 8)
= [(x2 + 2x) + (4x + 8)].(x2 + 5x + 8)
= [x(x + 2) + 4(x + 2)].(x2 + 5x + 8)
= (x + 2).(x + 4).(x2 + 5x + 8)
Chọn D.
Câu 2. Phân tích đa thức (x+ 1).(x+ 2). (x+ 3). (x+ 4) + 1 thành nhân tử
A. (x +1).(x+ 5). (x+ 6). (x- 1)
B. (x+ 2).(x- 3).(x + 7).(x – 1)
C. (x2 + 5x + 5)2
D. Đáp án khác
(x + 1).(x + 2).(x + 3).(x + 4) + 1
= [(x + 1).(x + 4)].[(x + 2).(x + 3)] + 1
= (x2 + 5x + 4).(x2 + 5x + 6) + +1
+ Đặt t = x2 + 5x + 5 => t - 1 = x2 + 5x + 4; t + 1 = x2 + 5x + 6
+ Ta có :
(x2 + 5x + 4).(x2 + 5x + 6) + 1
= (t - 1).(t + 1) + 1 = t2 - 1 + 1
= t2 = (x2 + 5x+ 5)2
Chọn C.
Câu 3. Phân tích đa thức x4 + 2x3 + 5x2 + 4x - 12 thành nhân tử
A. (x - 1).(x - 2).(x2 - x + 6)
B. (x - 1).(x + 2).(x2 + x + 6)
C. (x + 1).(x + 2).(x2 - x + 6)
D. Đáp án khác
• Ta có:
x4 + 2x3 + 5x2 + 4x - 12
= (x4 + 2x3 + x2) + (4x2 + 4x) - 12
= x2.(x2 + 2x + 1) + 4x(x + 1) - 12
= x2.(x + 1)2 + 4x.(x + 1) - 12
• Đặt t = x(x + 1) => t2 = x2.(x + 1)2
Do đó;
x2.(x + 1)2 + 4x.(x + 1) - 12 = t2 + 4t - 12
= (t2 + 6t) - (2t + 12) = t(t + 6) -2(t + 6) = (t - 2).(t + 6)
= [x.(x + 1) - 2].[x.(x + 1) + 6] = (x2 + x - 2).(x2 + x + 6)
= [(x2 - 1) + (x - 1)].(x2 + x + 6)
= [(x + 1).(x - 1) + 1.(x - 1)].(x2 + x + 6)
= (x - 1).(x + 1 + 1).(x2 + x + 6) = (x - 1).(x + 2).(x2 + x + 6)
Chọn B.
Câu 4. Phân tích đa thức (x + 1).(x + 3).(x + 5).(x + 7) + 15 thành nhân tử
A. (x + 6).(x + 2).(x2 + 8x + 10)
B. (x - 6).(x + 2).(x2 + 8x - 10)
C. (x + 6).(x - 2).(x2 - 8x + 10)
D. Đáp án khác
Ta có:
(x + 1).(x + 3).(x + 5).(x + 7) + 15
= [(x + 1).(x + 7)].[(x + 3).(x + 5)] + 15
= (x2 + 8x + 7).(x2 + 8x + 15) + 15
+ Đặt t = x2 + 8x + 11 =>t - 4 = x2 + 8x + 7; t + 4 = x2 + 8x + 15
Khi đó: (x2 + 8x + 7).(x2 + 8x + 15) + 15
= (t - 4).(t + 4) + 15
= t2 - 16 + 15 = t2 - 1 = (t + 1).(t - 1)
= (x2 + 8x + 11 + 1).(x2 + 8x + 11 - 1)
= (x2 + 8x + 12).(x2 + 8x + 10)
= [(x2 + 2x) + (6x + 12)].(x2 + 8x + 10)
= [x.(x + 2) + 6(x + 2)].(x2 + 8x + 10)
= (x + 6).(x + 2).(x2 + 8x + 10)
Chọn A.
Câu 5. Phân tích đa thức(x2 + 8x + 7).(x2 + 8x + 15) + 15 thành nhân tử
A. (x2 - 8x + 10).(x + 6).(x + 2)
B. (x2 + 8x + 10).(x + 6).(x + 2)
C. (x2 + 8x + 10).(x - 6).(x + 2)
D. Đáp án khác
Đặt t = x2 + 8x + 7 => t + 8 = x2 + 8x + 15
Ta có: (x2 + 8x + 7).(x2 + 8x + 15) + 15
= t.(t + 8) + 15 = t2 + 8t + 15
= (t2 + 5t) + (3t + 15)
= t(t + 5) + 3(t + 5) = (t + 3).(t + 5)
= (x2 + 8x + 7 + 3).(x2 + 8x + 7 + 5)
= (x2 + 8x + 10).(x2 + 8x + 12)
= (x2 + 8x + 10).[(x2 + 2x) + (6x + 12)]
= (x2 + 8x + 10).[(x(x + 2) + 6(x + 2)]
= (x2 + 8x + 10).(x + 6).(x + 2)
Chọn B.
Câu 6. Phân tích đa thức (x + 2). (x+ 3). (x+ 4).(x+ 5) - 24 thành nhân tử
A. (x2 - 7x + 16).(x + 6).(x + 1)
B. (x2 + 7x + 16).(9x - 6).(x + 1)
C. (x2 + 7x + 16).(x + 6).(x + 1)
D. Đáp án khác
Ta có: (x + 2). (x + 3). (x+ 4). (x+ 5) – 24
= [(x + 2).(x + 5)].[(x + 3).(x + 4)] - 24
= (x2 + 7x + 10).(x2 + 7x + 12) - 24
+ Đặt t = x2 + 7x + 11 => t - 1 = x2 + 7x + 10; t + 1 = x2 + 7x + 12
Khi đó:
(x2 + 7x + 10).(x2 + 7x + 12) - 24
= (t - 1).(t + 1) - 24
= t2 - 1 - 24 = t2 - 25 = (t + 5).(t - 5)
= (x2 + 7x + 11 + 5).(x2 + 7x + 11 - 5)
= (x2 + 7x + 16).(x2 + 7x + 6)
= (x2 + 7x + 16).[(x2 + x) + (6x + 6)]
= (x2 + 7x + 16).[x(x + 1) + 6(x + 1)]
= (x2 + 7x + 16).(x + 6).(x + 1)
Chọn C.
Câu 7. Phân tích đa thức thành nhân tử (x2 + 3)2 - x2 - 5
A. (x2 + 2).(x2 + 1)
B. (x2 + 4).(x2 + 2)
C. (x2 + 3).(x2 + 1)
D. (x2 + 4).(x2 + 1)
Đặt t = x2 + 3. Suy ra:
(x2 + 3)3 - x2 - 5 = (x2 + 3)2 - (x2 + 3) - 2
= t2 - t - 2 = (t2 - 1) - (t + 1)
= (t + 1).(t - 1) - (t + 1)
= (t + 1).(t - 1 - 1) = (t + 1).(t - 2)
= (x2 + 3 + 1).(x2 + 3 - 2) = (x2 + 4).(x2 + 1)
Chọn D.
Câu 8. Phân tích đa thức x4 - x2 - 6 thành nhân tử
A. (x2 - 2).(x2 + 3)
B. (x2 + 2).(x2 - 3)
C. (x2 - 2).(x2 - 3)
D. (x2 + 2).(x2 + 3)
Đặt t = x2, khi đó:
x4 - x2 - 6 = t2 - t - 6
= (t2 - 4) - (t + 2) = (t + 2).(t - 2) - 1.(t + 2)
= (t + 2).(t - 2 - 1) = (t + 2).(t - 3)
= (x2 + 2).(x2 - 3)
Chọn B.
Câu 9. Phân tích đa thức (x3 + 3)2 - 3(x3 + 3) + 2 thành nhân tử
A. (x3 + 2).(x + 1).(x2 - x + 1)
B. (x3 + 2).(x - 1).(x2 + x + 1)
C. (x3 - 2).(x + 1).(x2 - x + 1)
D. Đáp án khác
Đặt t = x3 + 3, ta có:
(x3 + 3)2 - 3(x3 + 3) + 2 = t2 - 3t + 2
= (t2 - t) - (2t - 2) = t(t - 1) - 2(t - 1)
= (t - 1).(t - 2)
= (x3 + 3 - 1).(x3 + 3 - 2)
= (x3 + 2).(x3 + 1) = (x3 + 2).(x + 1).(x2 - x + 1)
Chọn A.
Câu 10. Phân tích đa thức (3 - x3)2 + x3 - 9 thành nhân tử
A. (3 - x3).x3
B. -(5 - x3).x3
C. (6 - x3).x3
D. Đáp án khác
Đặt t = 3 -x3 => x3 = 3 - t
Ta có:
(3 - x3)2 + x3 - 9
= t2 + 3 - t - 9 = t2 - t - 6
= (t2 - 3t) + (2t - 6)
= t(t - 3) + 2(t - 3) = (t + 2).(t - 3)
= (3 - x3 + 2).(3 - x3 - 3)
= -(5 - x3).x3
Chọn B.

