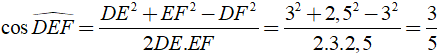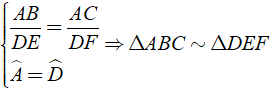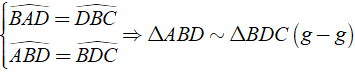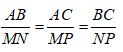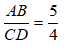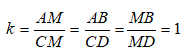Bài tập Các trường hợp đồng dạng của tam giác chọn lọc, có đáp án
Bài tập Các trường hợp đồng dạng của tam giác chọn lọc, có đáp án
Haylamdo biên soạn và sưu tầm Bài tập Các trường hợp đồng dạng của tam giác chọn lọc, có đáp án Toán lớp 8 tổng hợp bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm bài tập từ đó đạt điểm cao trong bài thi môn Toán lớp 8.
I. Bài tập trắc nghiệm
Bài 1: Cho Δ ABC vuông góc tại A có BC = 5cm, AC = 3cm, EF = 3cm, DE = DF = 2,5cm. Chọn phát biểu đúng?
A. Δ ABC ∼ Δ DEF
B. ABCˆ = EFDˆ
C. ACBˆ = ADFˆ
D. ACBˆ = DEFˆ
Áp dụng định lý Py – ta – go vào tam giác ABC vuông tại A ta được
BC2 = AC2 + AB2 ⇒ AB = √ (BC2 - AC2) = √ (52 - 32) = 4( cm )
Ta có: cos ACBˆ = AC/BC = 3/5
Xét tam giác DEF có:
Khi đó ACBˆ = DEFˆ
Chọn đáp án B.
Bài 2: Cho hai tam giác Δ RSK và Δ PQM có: RS/PQ = RK/PM = SK/QM thì:
A. Δ RSK ∼ Δ PQM
B. Δ RSK ∼ Δ MPQ
C. Δ RSK ∼ Δ QPM
D. Δ RSK ∼ Δ QMP
Ta có: RS/PQ = RK/PM = SK/QM ⇒ Δ RSK ∼ Δ PQM
Chọn đáp án A.
Bài 3: Nếu Δ RSK ∼ Δ PQM có: RS/PQ = RK/PM = SK/QM thì
A. RSKˆ = PQMˆ
B. RSKˆ = PMQˆ
C. RSKˆ = MPQˆ
D. RSKˆ = QPMˆ
Ta có Δ RSK ∼ Δ PQM ⇔ 
Chọn đáp án A.
Bài 4: Chọn câu trả lời đúng?
A. Δ ABC, Δ DEF;AB/DE = AC/DF;Bˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
B. Δ ABC, Δ DEF;AB/DE = AC/DF;Cˆ = Fˆ ⇒ Δ ABC ∼ Δ DEF
C. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Dˆ ⇒ Δ ABC ∼ Δ DEF
D. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
Ta có:
Chọn đáp án C.
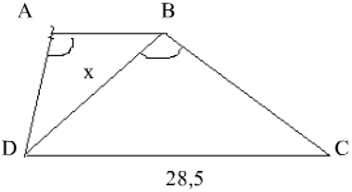
Bài 5: Cho hình bên, ABCD là hình thang ( AB//CD ) có AB = 12,5cm; CD = 28,5cm; DABˆ = DBCˆ. Tính độ dài đoạn BD gần nhất bằng bao nhiêu?
A. 17,5 B. 18
C. 18,5 D. 19
Xét Δ ABD và Δ BDC có:
⇒ AB/BD = AD/BC = BD/DC
hay 12,5/x = x/28,5 ⇒ x2 = 1425/4 ⇔ x ≈ 18,87
Chọn đáp án D.
Bài 6: Cho tam giác ABC có M và N lần lượt là trung điểm của AC và AB. Gọi AD là tia phân giác của góc BACˆ = DBCˆ, tia AD cắt MN tại P. Hỏi tam giác nào đồng dạng với tam giác ANP
A. Δ ABD B. ΔAMP
C. ΔABD D. Δ ACD
Xét tam giác ABC có M và N lần lượt là trung điểm của AC và AB nên MN là đường trung bình của tam giác ABC
Suy ra: MN // BC
Xét tam giác ABD có MP// BD (vì MN// BC)
Suy ra: Tam giác ANP đồng dạng với tam giác ABD.
Chọn đáp án A
Bài 7: Cho hình bình hành ABCD. Trên cạnh AB lấy điểm E, gọi F là giao điểm của DE và BC. Tìm khẳng định sai ?
A. Δ DAE đồng dạng Δ FBE
B. Δ DAE đồng dạng ΔFCD
C. Δ DEA đồng dạng ΔFCD
D. Δ FBE đồng dạng ΔFCD
* Xét tam giác DAE và ΔFBE có:
∠AED = ∠BEF (2 góc đối đỉnh)
∠ADE = ∠EFB (2 góc so le trong )
Suy ra: Δ DAE đồng dạng Δ FBE ( g.g) (1)
* Vì ABCD là hình bình hành nên: BE// CD
Suy ra: Δ FBE đồng dạng ΔFCD ( định lí) (2)
Từ (1) và (2) suy ra Δ DAE đồng dạng ΔFCD ( bắc cầu)
Chọn đáp án C
Bài 8: Cho tam giác ABC có AB = 3cm, AC = 4cm và BC = 5cm. Tam giác MNP vuông tại M có MN = 6cm; NP = 10cm . Tìm khẳng định sai?
A. Tam giác ABC là tam giác nhọn
B. Δ ABC đồng dạng tam giác MNP
C. Tam giác ABC vuông tại A.
D. MP = 8cm
* Ta có: AB2 + AC2 = BC2 (32 + 42 = 52 = 25 )
Suy ra: tam giác ABC vuông tại A.
* Áp dụng định lí Py ta go vào tam giác MNP ta có:
NP2 = MN2 + MP2
Suy ra: MP2 = NP2 – MN2 = 102 – 62 = 64
Do đó MP = 8cm.
*Ta có:
Do đó, Δ ABC đồng dạng tam giác MNP (c.c.c)
Chọn đáp án A
Bài 9: Cho tam giác ABC có M, N và P lần lượt là trung điểm của AB ; AC; BC. Tìm khẳng định sai
A. ΔAMN đồng dạng ΔABC ( định lí)
B. ΔCNP đồng dạng ΔCAB ( định lí)
C. ΔAMN đồng dạng ΔNPC
D. Chỉ có đúng 2 cặp tam giác đồng dạng .
* Xét tam giác ABC có M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC
Suy ra : MN// BC
Tương tự có NP // AB
* Xét Δ AMN và ΔNPC có:
∠MAN = ∠PNC ( hai góc đồng vị )
∠ANM = ∠NCP ( hai góc đồng vị)
Suy ra: Δ AMN đồng dạng ΔNPC (g.g)
* Vì MN// BC nên ΔAMN đồng dạng ΔABC ( định lí)
* Vì NP // AB nên Δ CNP đồng dạng Δ CAB ( định lí)
Chọn đáp án D
Bài 10: Cho tam giác ABC có M là trung điểm của AC. Lấy điểm D đối xứng với B qua M . Khi đó :
A. Tứ giác ABCD là hình thoi
B. AC = BD
C. ΔAMB = ΔCMD theo tỉ số đồng dạng k = 1
D. 
Xét Δ AMB và ΔCMD có:
AM = MC ( vì M là trung điểm của AC)
∠AMB = ∠CMD = 90o
BM = MD ( vì D đối xứng với B qua M)
Suy ra: Δ AMB = ΔCMD ( c.g.c)
Suy ra: Hai tam giác này cũng đồng dạng với nhau và tỉ số đồng dạng là:
D. 
Chọn đáp án C
