Các dạng bài tập Toán 8 Chương 2: Đa giác. Diện tích đa giác chọn lọc
Các dạng bài tập Toán 8 Chương 2: Đa giác. Diện tích đa giác chọn lọc
Haylamdo biên soạn và sưu tầm Các dạng bài tập Chương 2: Đa giác. Diện tích đa giác chọn lọc môn Toán lớp 8 sẽ giúp học sinh nắm vững lý thuyết, biết cách làm các dạng bài tập từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi môn Toán 8.
Mục lục Chương 2: Đa giác. Diện tích đa giác
I/ Lý thuyết & Bài tập theo bài học
- Lý thuyết Bài 1: Đa giác. Đa giác đều
- Bài tập Bài 1: Đa giác. Đa giác đều
- Lý thuyết Bài 2: Diện tích hình chữ nhật
- Bài tập Bài 2: Diện tích hình chữ nhật
- Lý thuyết Bài 3: Diện tích tam giác
- Bài tập Bài 3: Diện tích tam giác
- Lý thuyết Bài 4: Diện tích hình thang
- Bài tập Bài 4: Diện tích hình thang
- Lý thuyết Bài 5: Diện tích hình thoi
- Bài tập Bài 5: Diện tích hình thoi
- Tổng hợp Lý thuyết & Trắc nghiệm Chương 2 Hình học 8
II/ Các dạng bài tập
- Công thức, cách tính góc của đa giác hay, chi tiết
- Công thức, cách tính đường chéo của đa giác hay, chi tiết
- Công thức, cách tính góc của đa giác đều hay, chi tiết
- Công thức, cách tính diện tích hình chữ nhật, hình tam giác cực hay
- Cách tính độ dài đoạn thẳng bằng công thức tính diện tích
- Cách chứng minh đẳng thức hình học bằng cách sử dụng diện tích
- Tìm vị trí của một điểm thỏa mãn đẳng thức về diện tích
- Tìm giá trị lớn nhất, giá trị nhỏ nhất của diện tích một hình
- Công thức, cách tính diện tích hình thang, hình bình hành, hình thoi
- Chứng minh đẳng thức diện tích hình thang, hình bình hành, hình thoi
- Vận dụng công thức tính diện tích để tính toán và chứng minh đẳng thức
- Cách tính diện tích đa giác hay, chi tiết
- Dạng bài tập chứng minh bất đẳng thức diện tích
Dạng bài: Tính góc của đa giác
A. Phương pháp giải
+) Tổng các góc trong của đa giác n cạnh là (n-2).1800.
+) Để tìm số cạnh của đa giác khi biết tổng các góc, ta dùng công thức trên.
Tổng các góc ngoài của đa giác lồi cạnh có số đo là 3600 ( tại mỗi đỉnh chỉ chọn một góc ngoài).
B. Ví dụ minh họa
Câu 1: Tổng số đo các góc của đa giác đều 7 cạnh là:
A. 9000
B. 5400
C. 10800
D. 1080
Giải. Tổng số đo của các góc của đa giác đều 7 cạnh là: (7-2).1800 = 9000
Câu 2: Trong tất cả các góc trong và một góc ngoài của một đa giác có số đo là 47058,50. Hỏi đa giác đó có bao nhiêu cạnh?
Lời giải:
Gọi n là số cạnh của đa giác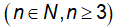 
Tổng số đo góc trong của đa giác bằng (n-2).1800
Vì tổng các góc trong và một trong các góc ngoài của đa giác có số đo là 47058,50 nên ta có:
Vậy số cạnh của đa giác là 263.
Câu 3: Tổng số đo các góc của một đa giác n – cạnh trừ đi góc A của nó bằng 5700. Tính số cạnh của đa giác đó và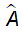 
.
Lời giải:
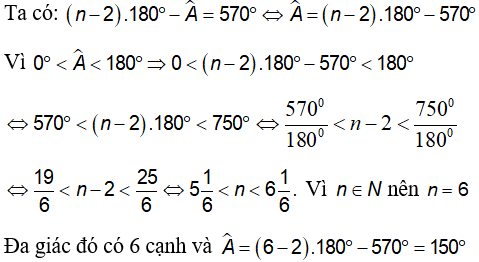
Dạng bài: Tính đường chéo của đa giác
A. Phương pháp giải
+) Số đường chéo của đa giác lồi n đỉnh là
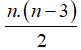
+) Để tìm số cạnh của đa giác khi biết số đường chéo, ta dùng công thức trên.
B. Ví dụ minh họa
Câu 1: Cho đa giác 8 cạnh, số đường chéo của đa giác đó là:
Lời giải:
Số đường chéo của đa giác lồi n cạnh là:
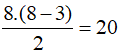
Câu 2: Tổng số đường chéo của ngũ giác lồi là:
A. 7
B. 8
C. 5
D. 10
Lời giải:
Số các đường chéo của đa giác lồi 5 cạnh bằng:
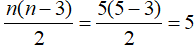
Câu 3: Một đa giác có 27 đường chéo. Hỏi đa giác có bao nhiêu cạnh?
Giải.
Gọi số cạnh của đa giác là n (cạnh;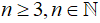 
) thì số đường chéo là
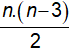
Theo giả thiết đa giác có 27 đường chéo nên ta có:
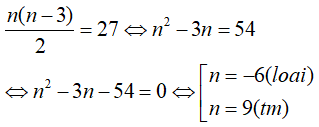
Vậy đa giác có 9 cạnh.
Câu 4: Tìm số cạnh của một đa giác biết số đường chéo hơn số cạnh là 7.
Giải.
Đặt số cạnh của đa giác là n (cạnh,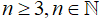 
) thì số đường chéo là
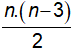
Theo đề bài số đường chéo hơn số cạnh là 7, ta có:
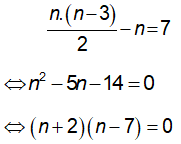
Vì n ≥ 3 nên n - 7 = 0 ⇔ n = 7. Vậy số cạnh của đa giác là 7.
Dạng bài: Tìm giá trị lớn nhất (nhỏ nhất) của diện tích một hình
A. Phương pháp giải
+) Nếu diện tích của một hình luôn lớn hơn hoặc bằng một hằng số m, và tồn tại một vị trí của hình để diện tích bằng m thì m là số đo diện tích nhỏ nhất của hình đó.
+) Nếu diện tích của một hình luôn nhỏ hơn hoặc bằng một hằng số M, và tồn tại một vị trí của hình để diện tích bằng M thì M là số đo diện tích lớn nhất của hình đó.
B. Ví dụ minh họa
Câu 1: Trong các hình chữ nhật có cùng chu vi là 100cm, hình có diện tích lớn nhất là bao nhiêu?
Lời giải:
Nửa chu vi của hình chữ nhật là: 100:2 = 50cm
Gọi kích thước của hình chữ nhật là x (cm; x>0) thì kích thước còn lại là 50-x (cm)
Diện tích hình chữ nhật là:
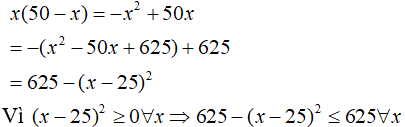
Dấu “=” xảy ra khi x = 25.
Vậy hình chữ nhật có diện tích lớn nhất là 252 = 625(cm2).
Câu 2: Cho đoạn thẳng AB có độ dài 2a. Vẽ về một phía của AB các tia Ax và By vuông góc với AB. Qua trung điểm M của AB có hai đường thẳng thay đổi luôn vuông góc với nhau và cắt Ax, By theo thứ tự tại C và D. Xác định vị trí của các điểm C, D sao cho tam giác MCD có diện tích nhỏ nhất. Tính diện tích tam giác đó?
Lời giải:
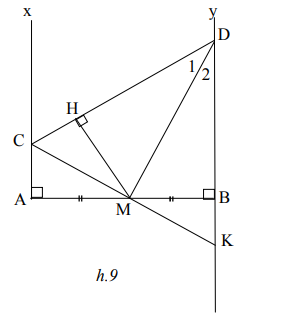
Lời giải:
Gọi K là giao điểm của CM và DB.
Xét ΔAMC và ΔBMK có:
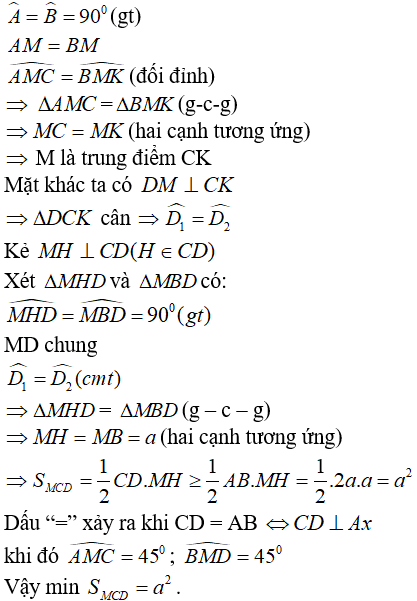
Các điểm C, D được xác định trên Ax; By sao cho AC = BC = a.
....................................
....................................
....................................
