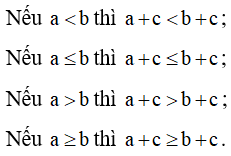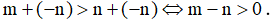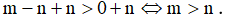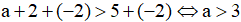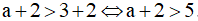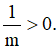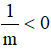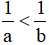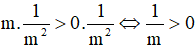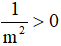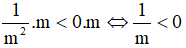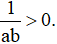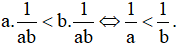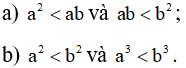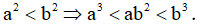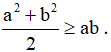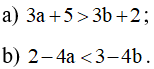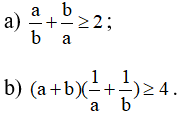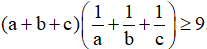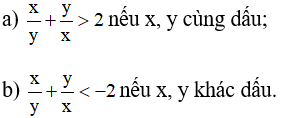Bài toán chứng minh bất đẳng thức lớp 8 cơ bản, chi tiết

Bài toán chứng minh bất đẳng thức lớp 8 cơ bản, chi tiết

Tài liệu Bài toán chứng minh bất đẳng thức lớp 8 cơ bản, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

Dạng bài: Bài toán chứng minh bất đẳng thức lớp 8 cơ bản, chi tiết

A. Phương pháp giải

a. Liên hệ giữa thứ tự và phép cộng

Haylamdo biên soạn và sưu tầm ba số a, b và c, ta có:

b. Liên hệ giữa thứ tự và phép nhân

*Với ba số a, b và c mà c > 0, ta có:

* Với ba số a, b và c mà c < 0, ta có:

B. Ví dụ minh họa

Câu 1:

a) Dựa vào tính chất liên hệ giữa thứ tự và phép cộng hãy chứng tỏ rằng nếu m > n thì m-n > 0.

b) Chứng tỏ nếu m-n > 0 thì m > n.

c) Chứng minh rằng từ a+2 > 5, suy ra a > 3. Điều ngược lại có đúng không?

Lời giải:

a) Từ m > n cộng cùng số -n vào 2 vế ta được

b) Cộng cùng số n vào 2 vế của m-n > 0 ta có

c) Từ a+2 > 5, cộng cùng số -2 vào 2 vế, ta được

Điều ngược lại là: từ a > 3 suy ra

Bằng cách cộng 2 vào hai vế của bất đẳng thức a > 3, rõ ràng điều ngược lại này cũng đúng.

Câu 2:

a) Cho bất đẳng thức m>0. Chứng tỏ

b) Cho bất đẳng thức m < 0. Chứng tỏ

c) Cho a>0, b>0 và a>b, chứng tỏ

Lời giải:

a) Từ m>0 , nhân cả hai vế với số 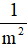ta được

b) Từ m<0 ta có 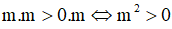, suy ra

Nhân cả hai vế của bất đẳng thức m<0 với số 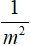ta được:

c) Do a>0, b>0 nên ab>0, suy ra

Từ a>b, nhân cả hai vế với cùng số 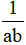ta có

Câu 3: Cho a>0, b>0, nếu a<b hãy chứng tỏ:

Lời giải:

a) Do a>0, b>0 nên từ a<b có

a²<ab(nhân cùng số dương a với 2 vế),

ab<b²(nhân cùng số dương b với 2 vế).

b) Từ câu (a), theo tính chất bắc cầu, suy ra a²<b². Khi đó:

C. Bài tập tự luyện

Câu 1: Cho a<b và c,d, chứng tỏ a+c<b+d.

Câu 2: Chứng tỏ rằng với a và b là các số bất kì thì:

Câu 3: Cho a>b chứng tỏ

Câu 4: Cho a và b là các số dương, chứng tỏ

Câu 5: Cho a, b, c là ba số dương. Chứng minh rằng

Câu 6: Cho x, y là hai số khác nhau và khác không. Chứng minh rằng: