Cách tìm giá trị lớn nhất, nhỏ nhất của biểu thức lớp 8 – dựa vào hằng đẳng thức
Cách tìm giá trị lớn nhất, nhỏ nhất của biểu thức lớp 8 – dựa vào hằng đẳng thức
Tài liệu Cách tìm giá trị lớn nhất, nhỏ nhất của biểu thức lớp 8 – dựa vào hằng đẳng thức Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.
A. Phương pháp giải
+ Với mọi x: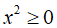 
+ Với mọi a; b ta có: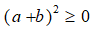 
. Dấu = xảy ra khi a+ b = 0
Và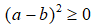 
. Dấu = xảy ra khi a- b = 0
• Cho biểu thức A(x):
+ Nếu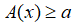 
thì giá trị nhỏ nhất của biểu thức A(x) là a.
+ Nếu 
thì giá trị lớn nhất của biểu thức A(x) là a.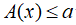
+ Nếu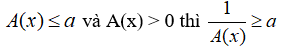 
+ Nếu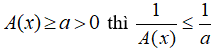 
+ Với mọi A; B ta có: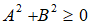 
B. Ví dụ minh họa
Ví dụ 1. Tìm giá trị lớn nhất của biểu thức: A = 6x - x2
A. 9 B. 11 C. 8 D. 13
Lời giải
Ta có:
A = 6x - x2 = -(x2 - 6x)
= -(x2 - 6x + 9) + 9
= -(x - 3)2 + 9
Haylamdo biên soạn và sưu tầm mọi x ta có: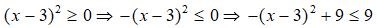 
Do đó, giá trị lớn nhất của biểu thức A là 9
Chọn A.
Ví dụ 2. Tìm giá trị lớn nhất của biểu thức B = 6 - 8x - x2
A. 6 B. 22 C. 18 D. 16
Lời giải
Ta có:
B = 6 - 8x - x2 = -(x2 + 8x) + 6
= -(x2 + 8x + 16) + 6 + 16
= -(x + 4)2 + 22
Vì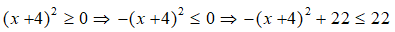 
Do đó, giá trị lớn nhất của biểu thức B là 22
Chọn B.
Ví dụ 3. Tìm giá trị nhỏ nhất của biểu thức C = 4x2 + 8x + 10
A . 6 B. 10 C. 12 D. 18
Lời giải
C = 4x2 + 8x + 10 = (2x)2 + 2.2x.2 + 4 + 6
= (2x + 2)2 + 6
Haylamdo biên soạn và sưu tầm mọi x ta có: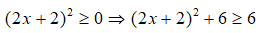 
Do đó, giá trị nhỏ nhất của biểu thức C là 6
Chọn A.
Ví dụ 4. Tìm giá trị lớn nhất của biểu thức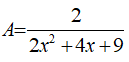 
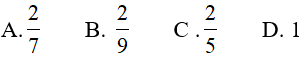
Lời giải
Ta có: 2x2 + 4x + 9 = (2x2 + 4x + 2) + 7 = 2(x2 + 2x + 1) + 7 = 2(x + 1)2 + 7
Haylamdo biên soạn và sưu tầm mọi x,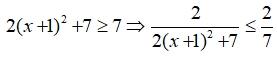 
Do đó, giá trị lớn nhất của A là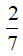 
.
Chọn A.
C. Bài tập trắc nghiệm
Câu 1. Tìm giá trị lớn nhất của biểu thức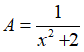 
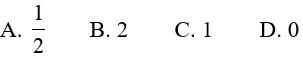
Haylamdo biên soạn và sưu tầm mọi x ta có: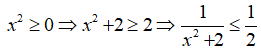 
Vậy giá trị lớn nhất của biểu thức A là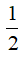 
Chọn A.
Câu 2. Tìm giá trị lớn nhất của biểu thức B = 10 - x2
A. 0 B.10 C. -10 D. 9
Ta có: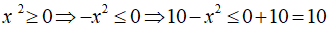 
Do đó, giá trị lớn nhất của biểu thức B là 10
Chọn B.
Câu 3. Tìm giá trị lớn nhất của biểu thức A = 4x - 2x2
A. 0 B. 1 C. 4 D. 2
Ta có;
A = 4x - 2x2 = -2(x2 - 2x)
= -2(x2 - 2x + 1) + 2 = -2(x - 1)2 + 2
Vì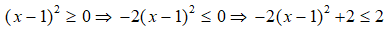 
Do đó, giá trị lớn nhất của biểu thức A là 2.
Chọn D.
Câu 4 . Tìm giá trị lớn nhất của biểu thức C = 4x + 3 - x2
A. 7 B. 4 C. 3 D. -1
Ta có:
Vì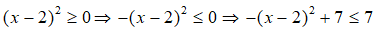 
Do đó, giá trị lớn nhất của C là 7.
Chọn A.
Câu 5. Tìm giá trị lớn nhất của biểu thức D = -x2 + 6x - 11
A. -11 B. 6 C. -2 D. 9
D = -x2 + 6x - 11 = -(x2 - 6x) - 11
= -(x2 - 6x + 9) + 9 - 11
= -(x - 3)2 - 2
Vì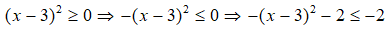 
Giá trị lớn nhất của biểu thức D là – 2
Chọn C
Câu 6. Tìm giá trị lớn nhất của biểu thức E = 4x - x2 + 1
A. 1 B. 5 C. 3 D. 6
Ta có:
E = 4x - x2 + 1 = -(x2 - 4x) + 1
= -(x2 - 4x + 4) + 4 + 1
= -(x - 2)2 + 5
Vì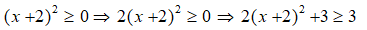 
Do đó, giá trị lớn nhất của biểu thức E là 5.
Chọn B.
Câu 7. Tìm giá trị nhỏ nhất của biểu thức A = 2x2 + 8x + 11
A. 3 B. 8 C. 11 D. 9
Ta có:
A = 2x2 + 8x + 11 = 2(x2 + 4x) + 11
= 2(x2 + 4x + 4) - 8 + 11
= 2(x + 2)2 + 3
Vì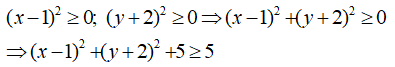 
Vậy giá trị nhỏ nhất của biểu thức A là 3
Chọn A.
Câu 8. Tìm giá trị nhỏ nhất của biểu thức E = x2 - 2x + y2 + 4y + 10
A. 1 B. 10 C. 5 D. 8
Ta có:
E = x2 - 2x + y2 + 4y + 10
= (x2 - 2x + 1) + (y2 + 4y + 4) + 5
= (x - 1)2 + (y + 2)2 + 5
Vì
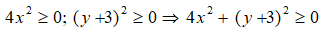
Do đó, giá trị nhỏ nhất của E là 5.
Chọn C.
Câu 9. Tìm giá trị nhỏ nhất của biểu thức D = 4x2 + y2 + 6y + 20
A. 20 B. 11 C. 10 D. 16
Ta có;
D = 4x2 + y2 + 6y + 20 = 4x2 + (y2 + 6y + 9) + 11
= 4x2 + (y + 3)2 + 11
Vì: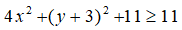 
Suy ra:
Vậy giá trị nhỏ nhất của D là 11
Chọn B.
Câu 10. Tìm giá trị nhỏ nhất của biểu thức G = x2 + 5y2 - 4xy - 8y + 28
A.10 B. 8 C. 20 D. 15
Ta có:
G = x2 + 5y2 - 4xy - 8y + 28
G = (x2 - 4xy + 4y2) + (y2 - 8y + 16) + 8
= (x - 2y)2 + (y - 4)2 + 8
Vì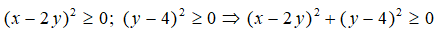 
Suy ra: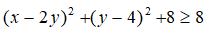 
Vậy giá trị nhỏ nhất của G là 8.
Chọn B.
