Chứng minh đẳng thức diện tích hình thang, hình bình hành, hình thoi

Chứng minh đẳng thức diện tích hình thang, hình bình hành, hình thoi

Tài liệu Chứng minh đẳng thức diện tích hình thang, hình bình hành, hình thoi Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

Dạng bài: Chứng minh đẳng thức diện tích

A. Phương pháp giải

+) Sử dụng các công thức diện tích

+) Vận dụng tính chất diện tích của đa giác.

B. Ví dụ minh họa

Câu 1: Cho hình thang ABCD (AB // CD, AB < CD). Gọi E và F tương ứng là trung điểm của AD và BC; gọi K và I tương ứng là hình chiếu vuông góc của E và F trên đường thẳng CD; gọi G và H tương ứng là hình chiếu vuông góc của E và F trên đường thẳng AB. Chứng minh S_ABCD = S_GHIK = KI. GK = EF. GK =1/2 (AB + CD). GK.

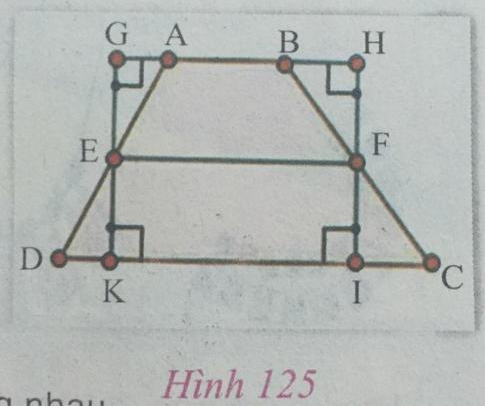
Giải.

Xét ΔEGA vuông tại G và ΔEKD vuông tại K, có:

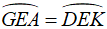
AE = DE (E là trung điểm AD)

⇒ ΔEGA = ΔEKD (cạnh huyền – góc nhọn)

Chứng minh tương tự, ta cũng có ΔFHB = ΔFIC.

Như vậy:

S_ABCD = S_DEK + S_CFI + S_ABFIKE = S_GAE + S_FHB + S_ABFIKE = S_GHIK = KI. GK = EF. GK (vì GHIK là hình chữ nhật do có 4 góc vuông). (1)

Lại có: EF là đường trung bình của hình thang ABCD nên EF = 1/2(AB + CD). (2)

Từ (1) và (2) ⇒ S_ABCD = S_GHIK = KI. GK = EF. GK = 1/2(AB + CD). GK.

Câu 2: Cho điểm O bất kì nằm trong hình bình hành ABCD. Chứng minh .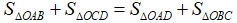

Giải.

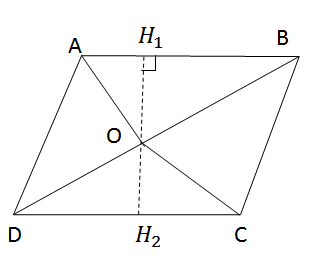
Từ O kẻ đường thẳng d vuông góc với AB ở H₁, cắt CD ở H₂.

Ta có OH₁ ⊥ AB

Mà AB // CD

Nên OH₂ ⊥ CD. Do đó:

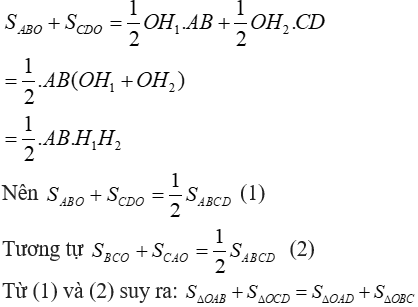
Câu 3: Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Vẽ 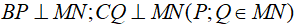. Chứng minh ?

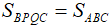Giải.

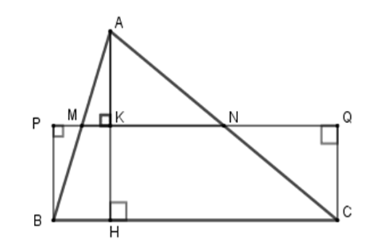
KẻAH⊥BC tại H và AH cắt MN tại K.

+ Xét tam giác ABC có MN là đường trung bình nên MN//BC suy ra AH⊥MN tại K.

Xét tứ giác CBPQ có PQ//BC (do MN//BC) và PB//CQ (do cùng vuông góc với PQ) nên CBPQ là hình bình hành. Lại có 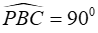nên tứ giác CBPQ là hình chữ nhật.

Suy ra S_CBPQ=BP.BC

+ Xét ΔBPM và ΔAKM có:

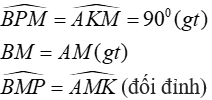
Suy ra ΔBPM=ΔAKM (cạnh huyền – góc nhọn)

⇒BP=AK (hai cạnh tương ứng) (1)

Xét ΔABK có MK//BH (do MN//BC) và M là trung điểm của AB nên K là trung điểm của AH (định lý về đường trung bình của tam giác). Nên AK=1/2 AH (2).

Từ (1) và (2) ta có PB=1/2 AH

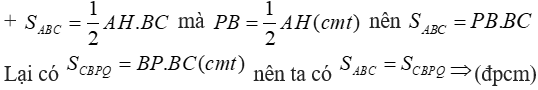
C. Bài tập tự luyện

Câu 1: Cho hình bình hành ABCD. Lấy M thuộc AB, N thuộc cạnh CD. Gọi P là giao điểm của AN và DM, Q là giao điểm của BN và CM.

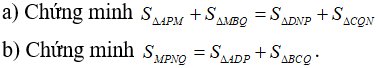
Câu 2: Cho hình thang ABCD (BC là đáy nhỏ). Gọi I là trung điểm của CD. Qua I kẻ đường thẳng d song song với AB. Kẻ AH và BE vuông góc với d. Chứng minh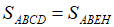

Câu 3: Trên đường chéo AC của hình vuông ABCD, lấy điểm E (E khác A và C). Qua E kẻ đường thẳng song song với các cạnh và cắt AB, BC, CD, DA lần lượt tại M, N, P, Q. So sánh diện tích MNPQ và diện tích ABCD.

Câu 4: Cho tam giác ABC vuông tại A. Về phía ngoài tam giác, vẽ các hình vuông ABDE, ACFG, BCHI. Chứng minh

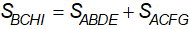
Câu 5: Cho hình bình hành ABCD. Gọi K, O, E, N là trung điểm của AB, BC, CD, DA. Các đoạn thẳng AO, BE, CN và DK cắt nhau tại L, M, R, P. Chứng minh

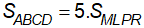
Câu 6: Cho hình bình hành ABCD. Gọi K và L là hai điểm thuộc cạnh BC sao cho BK = KL = LC. Tính tỉ số diện tích của:

a) Các tam giác DAC và DCK.

b) Tam giác DAC và tứ giác ADLB.

c) Các tứ giác ABKD và ABLD.

Câu 7: Cho hình thoi MNPQ. Biết A, B, C, D lần lượt là các trung điểm của các cạnh NM, NP, PQ, QM. Tính tỉ số diện tích của tứ giác ABCD và hình thoi MNPQ?