Cách chứng minh một số là nghiệm của một phương trình cực hay, có đáp án
Cách chứng minh một số là nghiệm của một phương trình cực hay, có đáp án
Tài liệu Cách chứng minh một số là nghiệm của một phương trình cực hay, có đáp án Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.
A. Phương pháp giải
• x0 là nghiệm của phương trình A(x) = B(x) ⇔ A(x0) = B(x0)
• x0 không là nghiệm của phương trình A(x) = B(x) ⇔ A(x0) ≠ B(x0)
B. Ví dụ minh họa
Ví dụ 1: Chứng minh x= -1 là nghiệm của phương trình 4x - 1 = 3x – 2
Hướng dẫn giải:
Thay x = -1 vào vế trái (VT) của phương trình ta được:
VT = 4.(-1)-1 = - 5
Thay x = -1 vào vế phải (VP) của phương trình ta được:
VP = 3.(-1) -2 = -5
Vì VT = VP nên x = -1 là nghiệm của phương trình đã cho.
Ví dụ 2: Xét xem x = 2 có là nghiệm của phương trình 3(2 - x) + 1 = 4 - 2x hay không?
Hướng dẫn giải:
Thay x = 2 vào phương trình
Ta có 3(2 – 2) +1 ≠ 4 - 2.2 ⇒ x = 2 không là nghiệm của phương trình đã cho.
Ví dụ 3: Xét xem x = -2 có là nghiệm của phương trình x2 – 3x -10 = 0 hay không?
Hướng dẫn giải:
Thay x = -2 vào phương trình ta được (-2)2 – 3.(-2) – 10 = 4 + 6 – 10 = 0
⇒ Vậy x = -2 là nghiệm của phương trình x2 – 3x -10 = 0
C. Bài tập vận dụng
Bài 1: Nghiệm của phương trình 2x + 1 = 3x – 1 là:
A. x = 1
B. x = 2
C. x = 3
D. x = 4
Đáp án: B.
Hướng dẫn giải:
Thay lần lượt các giá trị của x vào 2 vế của phương trình đã cho ta được
(A) Với x = 1 ; VT = 2.1 + 1= 3 ; VP = 3.1-1 = 2 ⇒ VT ≠ VP
(B) Với x = 2 ; VT = 2.2 + 1= 5 ; VP = 3.2 - 1 = 5 ⇒ VT = VP
(C) Với x = 3 ; VT = 2.3 + 1= 7 ; VP = 3.3 - 1 = 8 ⇒ VT ≠ VP
(D) Với x = 4 ; VT = 2.4 + 1= 9 ; VP = 3.4 -1 = 11 ⇒ VT ≠ VP
Vậy giá trị x = 2 là nghiệm của phương trình đã cho.
Bài 2: Số nào trong các số sau là nghiệm của phương trình 3x +7 = 1 + 2x .
A. -1.
B. 2
C. - 6
D. 6.
Đáp án: C
Hướng dẫn giải:
Thay lần lượt các giá trị của x vào 2 vế của phương trình đã cho ta được
(A) Với x = -1 ; VT = 3.(-1) + 7= 4 ; VP = 1 + 2.(-1) = -1 ⇒ VT ≠ VP
(B) Với x = 2 ; VT = 3.2 + 7 = 13 ; VP = 1 + 2.2 = 5 ⇒ VT ≠ VP
(C) Với x = -6 ; VT = 3.(-6) + 7 = -11 ; VP = 1 + 2.(-6) = -11 ⇒ VT = VP
(D) Với x = 6 ; VT = 3.6 + 7 = 25 ; VP = 1 + 2.6 = 13 ⇒ VT ≠ VP
Vậy giá trị x = -6 là nghiệm của phương trình đã cho.
Bài 3: Số nào trong các số sau là nghiệm của phương trình - 3x - 5 = 2(x - 1).
Đáp án: C
Hướng dẫn giải:
Thay lần lượt các giá trị của x vào 2 vế của phương trình đã cho ta được
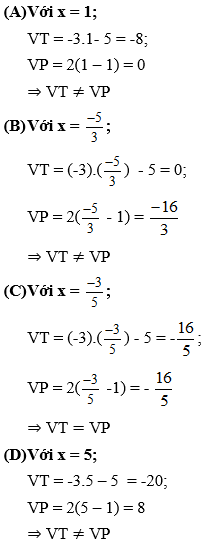
Vậy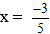 
là nghiệm của phương trình đã cho.
Bài 4: Giá trị x = -1 là nghiệm của phương trình nào trong các phương trình sau:
A. x + 2 = 3x - 1
B. 2x + 3 = 5x – 2
C. 2(x + 3) = 4
D. 5x - 1 = 3x + 2.
Đáp án: C
Hướng dẫn giải:
Thay x = -1 vào hai vế của các phương trình ta được:
PT (A): VT = -1 + 2 = 1; VP = 3(-1) – 1 = - 4
Vì VT ≠ VP nên x = -1 không là nghiệm của Pt (A)
PT (B): VT = 2(-1) + 3 = 1; VP = 5(-1) -2 = -7
Vì VT ≠ VP nên x = -1 không là nghiệm của Pt (B)
PT (C): VT= 2((-1) + 3)) = 2.2 = 4;
Vì VT = VP nên x = -1 là nghiệm của Pt (C)
PT(D): VT = 5(-1) – 1 = - 6; VP = 3(-1) + 2 = -1
Vì VT ≠ VP nên x = -1 không là nghiệm của Pt (D)
Vậy x = -1 là nghiệm của phương trình 2(x + 3) = 4.
Bài 5: Giá trị x = 3 là nghiệm của phương trình nào trong các phương trình sau:
A. 2x + 2 = 3(x – 1)
B. 2x2 + 3 = 5x – 2
C. 2(x + 3) = 4x + 2
D. x3 + 6 = 3x2 + 2x.
Đáp án: D
Hướng dẫn giải:
Thay giá trị x = 3 vào hai vế của các phương trình ta được:
PT (A): VT = 2.3 + 2 = 8; VP = 3(3 – 1) = 3.2 = 6
Vì VT ≠ VP. Nên x = 3 không là nghiệm của PT (A)
PT(B): VT = 2.32 + 3 = 2.9 + 3 = 21; VP = 5.3 – 2 = 15 – 2 = 13
Vì VT ≠ VP. Nên x = 3 không là nghiệm của PT (B)
PT (C): VT = 2(3 + 3) = 2.6 = 12; VP = 4.3 + 2 = 12 + 2 = 14
Vì VT ≠ VP. Nên x = 3 không là nghiệm của PT (C)
PT(D): VT = 33 + 6 = 27 + 6 = 33; VP = 3.32 + 2.3 = 3.9 + 6 = 33
Vì VT = VP. Nên x = 3 là nghiệm của PT (D)
Vậy x = 3 là nghiệm của phương trình x3 + 6 = 3x2 + 2x.
Bài 6: Chứng minh x = -1 là nghiệm của phương trình 5x + (x – 1) = -7
Hướng dẫn giải:
Thay x = -1 vào vế trái của PT ta được VT= 5(-1) + (-1– 1) = (-5) + (-2) = -7
Vì VT =VP
Vậy x = -1 là nghiệm của phương trình 5x + (x – 1) = -7
Bài 7: Xét xem x = -2 có là nghiệm của phương trình 2 – x + x2 = - 2x - 4 hay không?
Hướng dẫn giải:
Thay x = -2 vào phương trình
Ta được VT = 2 –(-2) + (-2)2 = 2 + 2 + 4 = 8; VP = -2(-2) – 4 = 0
⇒ VT ≠ VP (8 ≠ 0)
Vậy x = -2 không là nghiệm của phương trình đã cho.
Bài 8: Xét xem x = -1 có là nghiệm của phương trình (x + 1)(x - 2)(x + 5) = 0 hay không?
Hướng dẫn giải:
Thay x = -1 vào phương trình
Ta được VT= (-1 + 1)(-1 – 2)(-1 + 5) = 0.(-3).4 = 0= VP
Vậy x = -1 là nghiệm của phương trình đã cho.
Bài 9: Xét xem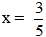 
có là nghiệm của phương trình (10x + 1)(3x + 2) – 5(x + 2) = 40
Hướng dẫn giải:
Thay 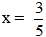vào 2 vế của phương trình
Ta được:
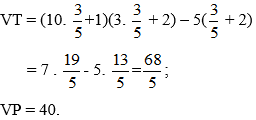
⇒ VT ≠ VP
Vậy 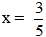không là nghiệm của phương trình đã cho.
Bài 10: Xét xem x = 1 có là nghiệm của phương trình 2(2x + 1) + 18 = 3(x + 2)(2x + 1) hay không?
Hướng dẫn giải:
Thay x = 1 vào 2 vế của phương trình
Ta được VT= 2(2.1 + 1) + 18 = 2.3 + 18 = 24; VP = 3(1 + 2)(2.1 + 1) = 3.3.3 = 27
VT ≠ VP
Vậy x = 1 không là nghiệm của phương trình đã cho.
