Các dạng bài tập về góc trong tứ giác và cách giải
Các dạng bài tập về góc trong tứ giác và cách giải
Tài liệu Các dạng bài tập về góc trong tứ giác và cách giải Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.
I. Kiến thức cần nhớ
1. Định nghĩa tứ giác
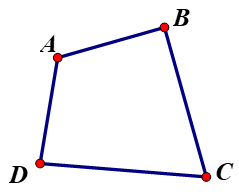
+ Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
+ Tứ giác ABCD trên gọi là tứ giác lồi.
+ Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác.
Chú ý: Nếu chỉ nhắc đến tứ giác, ta hiểu đó là tứ giác lồi.
2. Tính chất của tứ giác
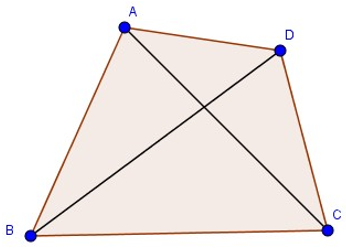
a) Tính chất đường chéo
Người ta chứng minh được rằng:
+ Trong một tứ giác lồi, hai đường chéo cắt nhau tại một điểm thuộc miền trong của tứ giác.
+ Ngược lại, nếu một tứ giác có hai đường chéo cắt nhau tại một điểm thuộc miền trong của nó thì tứ giác ấy là tứ giác lồi.
b) Tính chất góc
Định lý: Tổng các góc của một tứ giác bằng 3600 .
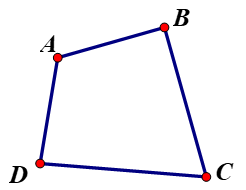
Tứ giác ABCD có: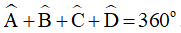 
Chú ý: Góc ngoài của tứ giác là góc kề bù với một góc của tứ giác.
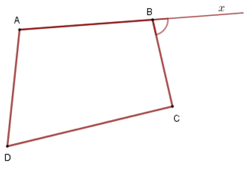
Góc CBx là góc ngoài tại đỉnh B của tứ giác ABCD nên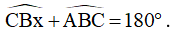 
II. Ví dụ minh họa
Dạng 1. Tính số đo các góc của tứ giác
Phương pháp giải: Áp dụng định lý tổng các góc của một tứ giác bằng 3600.
Ví dụ: Cho tứ giác ABCD có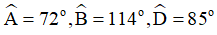 
. Tính số đo góc C.
Lời giải:
Áp dụng định lý tổng các góc của tứ giác bằng khi đó tứ giác ABCD có:
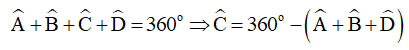
Thay số ta được: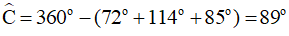 
Dạng 2. Chứng minh bài toán dựa vào định lý tổng các góc trong tứ giác
Phương pháp giải: Vận dụng định lí kết hợp với các tính chất khái niệm đã học như hai đường thẳng song song, hai tam giác bằng nhau...
Ví dụ 1: Cho tứ giác ABCD có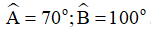 
. Các tia phân giác của góc C và D cắt nhau tại O. Tính số đo 
.
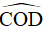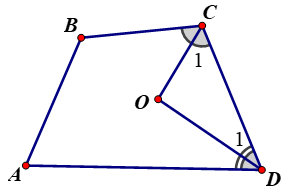
Lời giải:
Áp dụng định lý tổng các góc của tứ giác bằng 3600 khi đó tứ giác ABCD có:
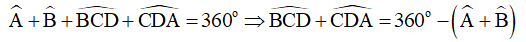
Thay số ta được: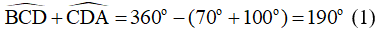 
Vì CO, DO lần lượt là tia phân giác của góc BCD và góc CDA nên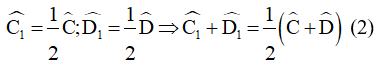 
Thay (1) vào (2) ta được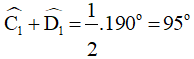 
Áp dụng định lý tổng ba góc của tam giác COD có: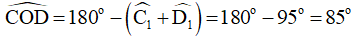 
Vậy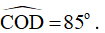 
Ví dụ 2: Chứng minh định lý mở rộng: Tổng bốn góc ngoài ở bốn đỉnh của một tứ giác bằng 3600 (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài).
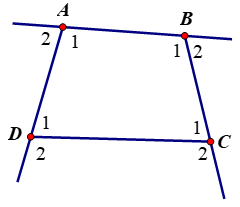
Lời giải:
Gọi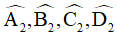 
là các góc ngoài của tứ giác ABCD. Khi đó 
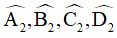lần lượt kề bù với 
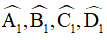. Vậy ta có:
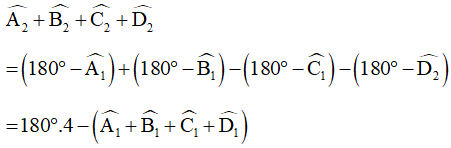
Áp dụng định lý tổng 4 góc cho tứ giác ABCD ta có:
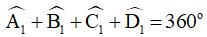
Khi đó: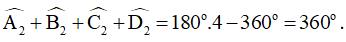 
Vậy tổng bốn góc ngoài ở bốn đỉnh của một tứ giác bằng 3600 .
III. Bài tập tự luyện
Bài 1. Điền vào chỗ chấm đáp án chỉ số đo x tương ứng với mỗi hình vẽ:
a)
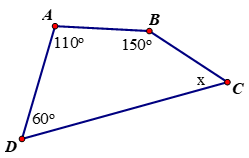
x = …...
b)
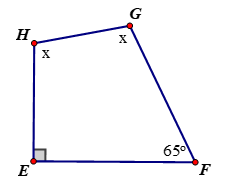
x = ……
c)
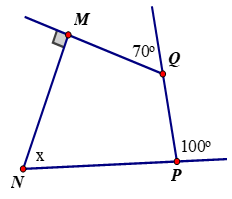
x = ……
Bài 2. Tứ giác ABCD có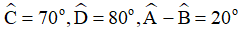 
. Tính số đo các góc A và B.
Bài 3. Cho tứ giác ABCD biết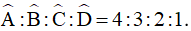 
a) Tính các góc của tứ giác ABCD.
b) Các tia phân giác của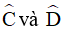 
cắt nhau tại E. Các đường phân giác của góc ngoài tại các đỉnh C và D cắt nhau tại F. Tính số đo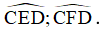 
Bài 4. Tính số đo các góc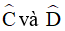 
của tứ giác ABCD biết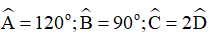 
Bài 5. Cho tứ giác ABCD có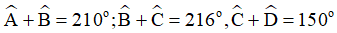 
. Tính số đo các góc của tứ giác ABCD.
Bài 6. Cho tứ giác ABCD có AB = AD, CB = CD.
a) Chứng minh AC là đường trung trực của BD;
b) Tính số đo 
biết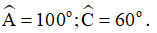 
Bài 7. Tứ giác MNPQ có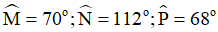 
. Tính số đo góc ngoài tại đỉnh Q.
Bài 8. Tứ giác ABCD có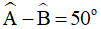 
. Các tia phân giác của cắt nhau tại I và 
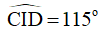. Tính các góc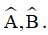 
Bài 9. Tứ giác ABCD có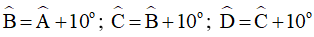 
. Tính số đo các góc của tứ giác.
Bài 10. Chứng minh rằng các góc của một tứ giác không thể đều là góc nhọn, không thể đều là góc tù.
Bài 11. Cho tứ giác ABCD, biết AB = AD,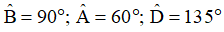 
a) Tính góc C và chứng minh rằng BD = BC.
b) Từ A kẻ AE ⊥ CD tại E, tính các góc của ΔAEC .
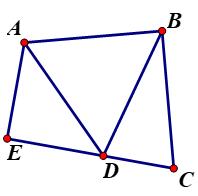
Bài 12. Cho tứ giác ABCD có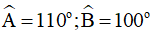 
. Các tia phân giác của góc C và D cắt nhau ở E. Các đường phân giác của góc ngoài tại các đỉnh C và D cắt nhau ở F. Tính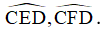 
Bài 13. Cho tứ giác ABCD, AB cắt CD tại E, BC cắt AD tại F. Các tia phân giác của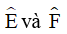 
cắt nhau tại I. Chứng minh:
a)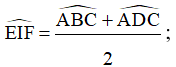 
b) Nếu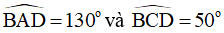 
thì IE ⊥ IF .
