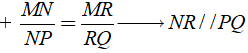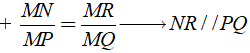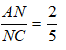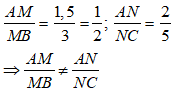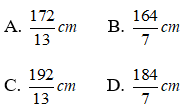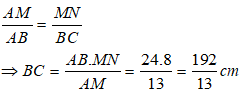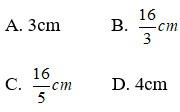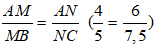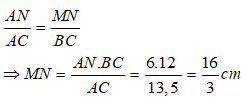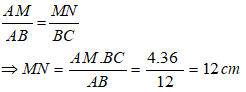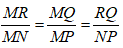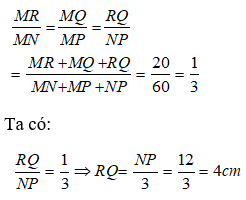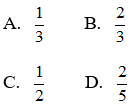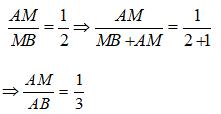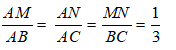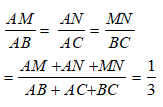Bài tập Định lí đảo và hệ quả của định lí Ta-lét chọn lọc, có đáp án
Bài tập Định lí đảo và hệ quả của định lí Ta-lét chọn lọc, có đáp án
Tài liệu Bài tập Định lí đảo và hệ quả của định lí Ta-lét chọn lọc, có đáp án Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.
I. Bài tập trắc nghiệm
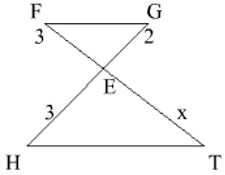
Bài 1: Tính x trong trường hợp sau biết rằng FG // HT :
A. x = 4,5 B. x = 3
C. x = 2 D. Cả 3 đáp án trên đều sai
Áp dụng hệ quả của định lí Ta – lét với FG//HT ta có:
FG//HT ⇒ EF/ET = EG/HE ⇔ ET = (EF.HE)/EG = (3.3)/2 = 4,5
Chọn đáp án A.
Bài 2: Cho hình bên. Chọn câu trả lời đúng?
A.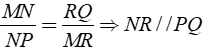 
B.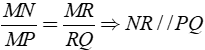 
C.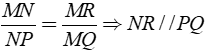 
D. Cả 3 đáp án đều sai.
Ta có:
Cả 3 đáp án A, B, C đều sai.
Chọn đáp án D.
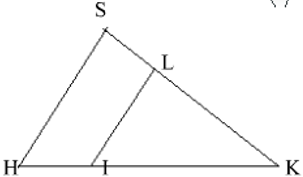
Bài 3: Cho hình bên. Chọn câu trả lời đúng?
A. SL/LK = HI/HK ⇒ SH//LI
B. SL/SK = HI/HK ⇒ SH//LI
C. HI/HK = LK/SL ⇒ SH//LI
D. HK/HI = SL/SK ⇒ SH//LI
Ta có:
+ SL/LK = HI/IK → SH//LI
+ SL/SK = HI/HK → SH//LI
Chọn đáp án B.
Bài 4: Cho Δ ABC có độ dài các cạnh như hình vẽ Kết quả nào sau đây đúng?
A. ED/BC = 1,5 B. ED/BC = 3/7,5
C. ED/BC = 3/5 D. Cả 3 đáp án đều sai.
Ta có: ED//BC ⇒ ED/BC = AE/AB = AD/AC = 3/5
Chọn đáp án C.
Bài 5: Cho tam giác ABC có AB = 4,5 cm. Một đường thẳng d cắt đoạn AB, AC lần lượt tại M và N sao cho AM = 1,5cm, AN = 2 cm và NC = 5cm. Tìm khẳng định sai ?
A. MN// BC
B. MB = 3cm
C. Đường thẳng MN và BC có điểm chung.
D. 
Vì điểm M nằm giữa hai điểm A và B nên:
MB = AB – AM = 4,5 - 1,5 = 3cm
Ta có:
Do đó, đường thẳng MN không song song với BC.
Chọn đáp án A
Bài 6: Cho tam giác ABC, một đường thẳng d song song với BC cắt 2 cạnh AB và AC lần lượt tại M và N sao cho AM = 13cm, MB = 11cm và MN = 8cm. Tính BC
Do M nằm giữa A và B nên: AB = AM + MB = 13 + 11 = 24 cm
Theo hệ quả định lí Ta let ta có:
Chọn đáp án C
Bài 7: Cho tam giác ABC, một đường thẳng d cắt 2 cạnh AB và AC tại M và N sao cho AM = 4cm, MB = 5cm, AN = 6 cm và AC = 13,5cm; BC = 12 cm . Tính MN?
Do N nằm giữa A và C nên: NC = AC - AN = 13,5 - 6 = 7,5cm
Ta có:
Suy ra: MN // BC ( định lí Ta let đảo)
Theo hệ quả định lí ta let ta có;
Chọn đáp án B
Bài 8: Cho tam giác ABC, đường thẳng d song song BC cắt hai cạnh AB và AC tại M và N sao cho AM = 4cm, MB = 8cm và BC = 36cm. Tính MN?
A. 10cm B. 8cm
C. 12cm D. Đáp án
Điểm M nằm giữa A và B nên: AB = AM + MB = 4 + 8 = 12cm
Áp dụng hệ quả định lí Ta let ta có;
Chọn đáp án C
Bài 9: Cho tam giác MNP, đường thẳng d song song với NP cắt hai cạnh MN và MP lần lượt tại R và Q. Chu vi tam giác MNP là 60cm và chu vi tam giác MQR là 20cm, PN = 12cm . Tính RQ?
A. 2cm B. 2,5cm
C. 3cm D. 4cm
Xét tam giác MNP có QR // NP , áp đụng hệ quả định lí Ta- let ta có:
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Chọn đáp án D
Bài 10: Cho tam giác ABC, đường thẳng d song song với BC cắt 2 cạnh AB và AC lần lượt tại M và N. Biết rằng
. Tỉnh tỉ số chu vi tam giác AMN và ABC ?
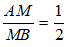
Ta có:
Vì MN// BC nên theo hệ quả định lí Ta let ta có:
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Do đó, tỉ số chu vi tam giác AMN và ABC là 1/3
Chọn đáp án A
