Chứng minh quan hệ song song, vuông góc, bằng nhau trong hình chóp đều
Chứng minh quan hệ song song, vuông góc, bằng nhau trong hình chóp đều
Tài liệu Chứng minh quan hệ song song, vuông góc, bằng nhau trong hình chóp đều Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

Dạng bài: Chứng minh các quan hệ song song, vuông góc, bằng nhau trong hình chóp đều
A. Phương pháp giải
+) Vận dụng các dấu hiệu nhận biết các quan hệ song song, vuông góc.
+) Chú ý rằng trong hình chóp đều thì:
- Các cạnh đáy bằng nhau.
- Các cạnh bên bằng nhau.
- Các trung đoạn bằng nhau.
B. Ví dụ minh họa
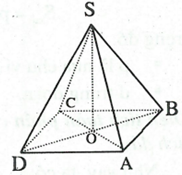
Câu 1: Cho hình chóp tứ giác đều S. ABCD, gọi O là giao điểm của AC và BD.
a) Chứng minh rằng 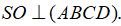
b) Chứng minh rằng 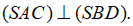
Lời giải:
|
a) Ta lần lượt có:
Từ (1), (2) suy ra b. Từ kết quả câu a), ta có: Mặt khác, vì ABCD là hình vuông nên |
|
Từ (3) và (4) suy ra: 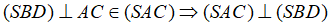
Câu 2: Cho hình hộp chữ nhật ABCD.A1B1C1D1 có ABCD là hình vuông. Gọi O là giao điểm của AC và BD, O1 là giao điểm của A1C1 và B1D1. Chứng minh rằng:
a) BDD1B1 là hình chữ nhật.
b) OO1⊥ (ABCD)
Lời giải:
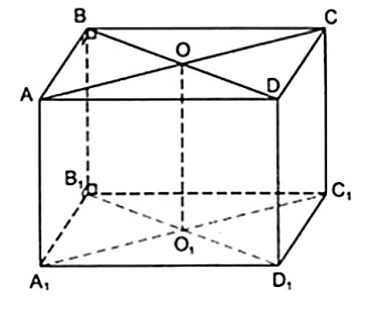
a) Từ giả thiết ABCD.A1B1C1D1 là hình hộp chữ nhật nên các mặt bên ( BB1A1A ),( BB1C1C ) là hình chữ nhật, do đó ta có:
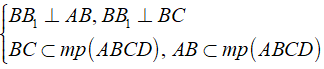
⇒ BB1⊥ mp (ABCD)
Mặt khác đường chéo BD ⊂ mp (ABCD) và đi qua B nên:
BB1⊥ BD ⇒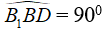
Chứng minh tương tự như trên, ta cũng được: 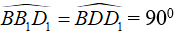
Điều đó chứng tỏ tứ giác BDD1B1 có ba góc vuông nên là hình chữ nhật.
b) Chứng minh tương tự như câu a, ta có tứ giác ACC1A1 là hình chữ nhật
Áp dụng tính chất đường chéo và các hình vuông ABCD, A1B1C1D1 ta được O là trung điểm của AC và BD và O1 là trung điểm của A1C1 và B1D1
⇒ OO1 là đường trung bình của các hình chữ nhật BDD1B1 và ACC1A1
Do đó: OO1//BB1//DD1//AA1//CC1
Suy ra: 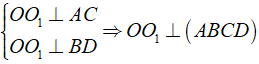
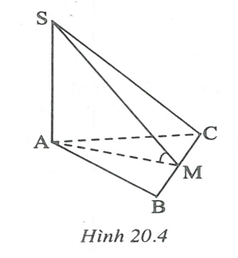 Câu 3: Cho hình chóp S.ABC có đáy là tam giác đều và SA là đường cao của hình chóp. Gọi M là trung điểm của BC.
Câu 3: Cho hình chóp S.ABC có đáy là tam giác đều và SA là đường cao của hình chóp. Gọi M là trung điểm của BC.
a) Chứng minh rằng 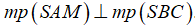
b) Cho biết 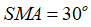 chứng minh rằng diện tích tam giác BCS bằng tổng diện tích của các tam giác ABS và ACS.
chứng minh rằng diện tích tam giác BCS bằng tổng diện tích của các tam giác ABS và ACS.
Giải.
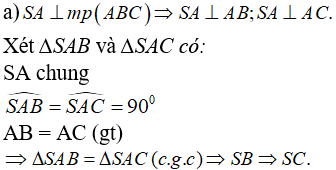
Xét ∆SBC cân tại S có M là trung điểm BC
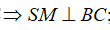 (1)
(1)
Xét ∆ABC đều có M là trung điểm BC.
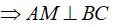 (2)
(2)
Từ (1), (2) 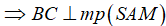
Mặt khác 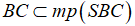 nên
nên 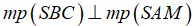
b) Xét ∆SAM vuông tại A,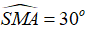 nên
nên 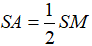 hay SM=2SA
hay SM=2SA
Diện tích ∆BCS là: 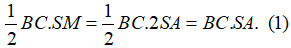
Tổng diện tích các ∆ABS và ∆ACS là:
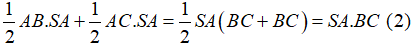
Từ (1) và (2) suy ra điều phải chứng minh.
C. Bài tập tự luyện
Câu 1: Cho hình chóp đều tam giác S.ABC. Gọi M, N, D và E lần lượt là trung điểm của AB, AC, SB và SC. Gọi O là giao điểm của BN và CM.
a) Chứng minh rằng tứ giác EDMN là hình bình hành;
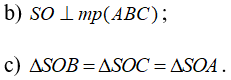
Câu 2: Cho hình chóp tứ giác đều S. ABCD, đường cao SO. Gọi M là trung điểm BC. Chứng minh rằng:
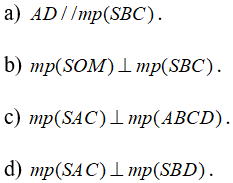
Câu 3: Cho hình chóp tứ giác đều S. ABCD. Gọi E, F, M lần lượt là trung điểm của SA, SD và BC. Chứng minh rằng:
a) CF//EM.
b) Tứ giác FEBC là hình thang cân.
Câu 4: Cho hình chóp tam giác đều S.ABC. Gọi G và H thứ tự là trọng tâm của các tam giác ABC, SBC.
a) Chứng minh rằng GH//SA.
b) GH song song với những mặt phẳng nào?
Câu 5: Cho hình chóp tứ giác đều S. ABCD. Trên các cạnh SA, SB, SC, SD lần lượt lấy các điểm A', B', C', D' sao cho Sa'=SB'=SC'=SD'. Chứng minh rằng:
a) Bốn điểm A', B', C, D' cùng thuộc một mặt phẳng. Có nhận xét gì về mặt phẳng (A'B'C'D') và mp(ABCD).
b) 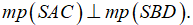
Câu 6: Cho hình chóp tứ giác đều S. ABCD. Cho biết 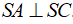 . Chứng minh rằng các mặt bên là những tam giác đều.
. Chứng minh rằng các mặt bên là những tam giác đều.
Câu 7: Cho hình chóp tam giác đều S.ABC, các mặt bên là những tam giác vuông cân tại S.
a) Chứng minh rằng mỗi mặt bên vuông góc với hai mặt bên còn lại.
b) Gọi độ dài của mỗi cạnh đáy là a, Tính chiều cao của hình chóp.

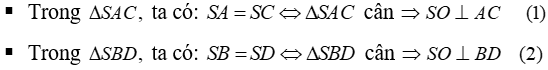
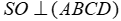
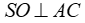 (3)
(3)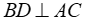 (4)
(4)