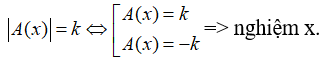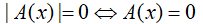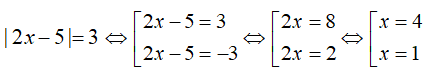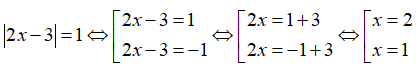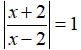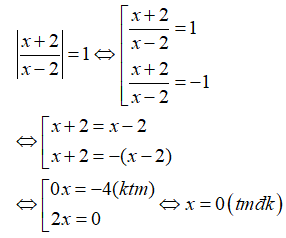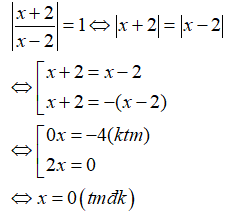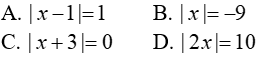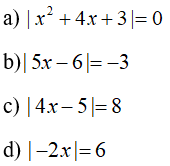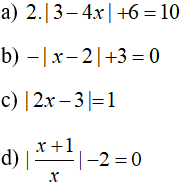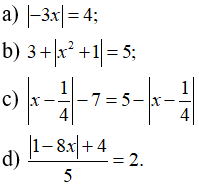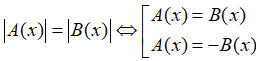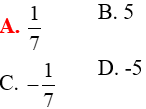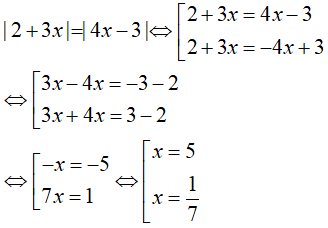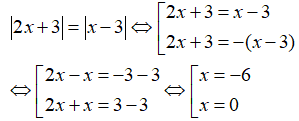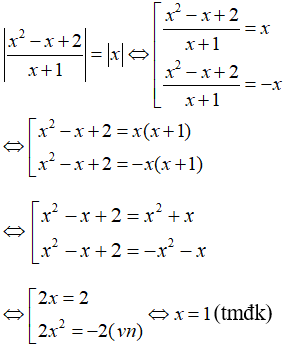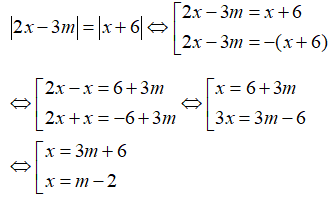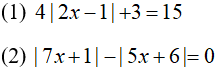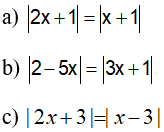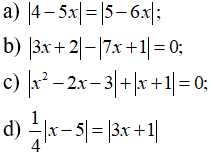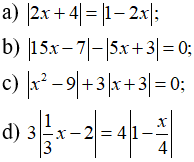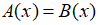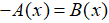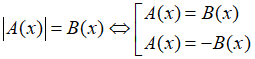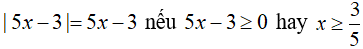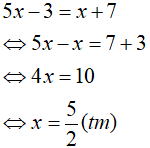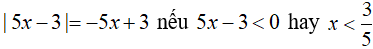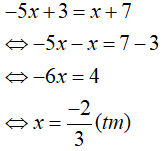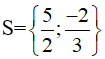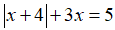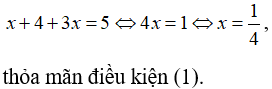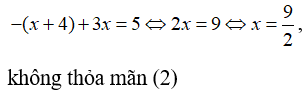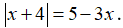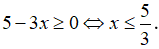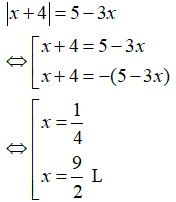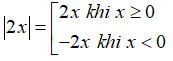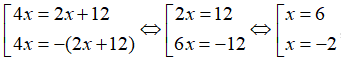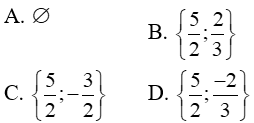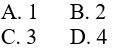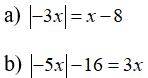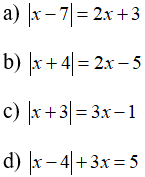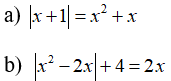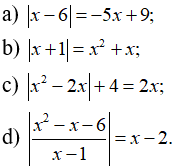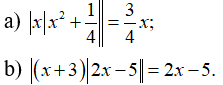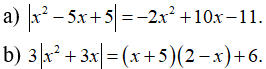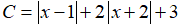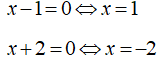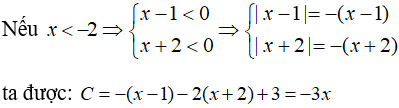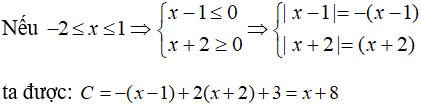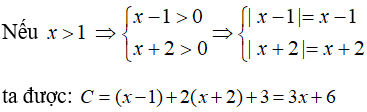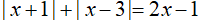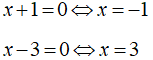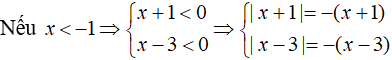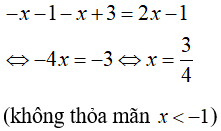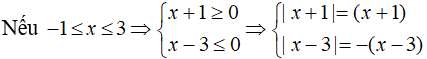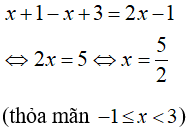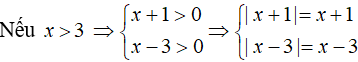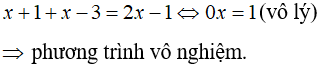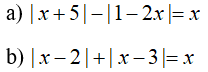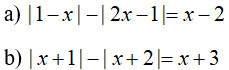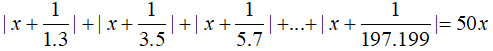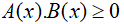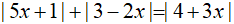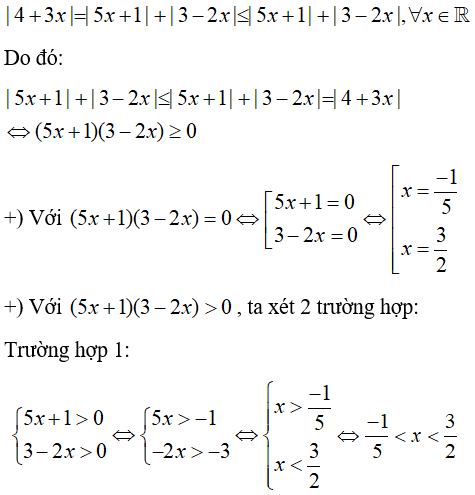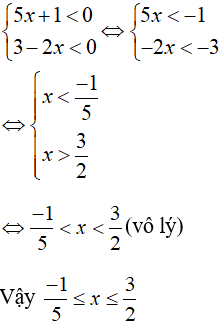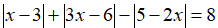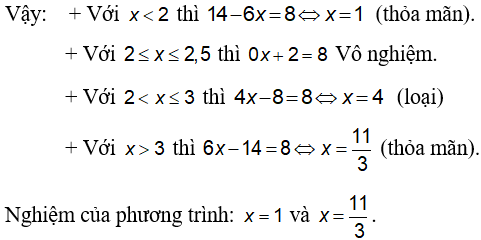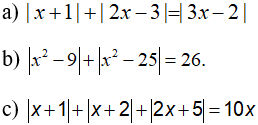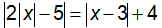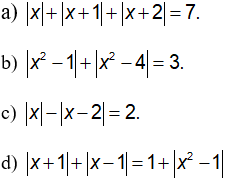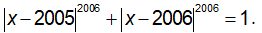Cách giải phương trình chứa dấu giá trị tuyệt đối hay, chi tiết

Cách giải phương trình chứa dấu giá trị tuyệt đối hay, chi tiết

Tài liệu Cách giải phương trình chứa dấu giá trị tuyệt đối hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

Dạng 1: Giải phương trình |A(x)| = k với k là hằng số, x là biến số

A. Phương pháp giải

Cách giải phương trình |A(x)| = k với k là hằng số, x là biến số:

+) Nếu k<0 thì phương trình vô nghiệm.

+) Nếu k>0

Bước 1: Đặt điều kiện để f(x) xác định (nếu cần).

Bước 2: Khi đó:

Bước 3: Kiểm tra điều kiện, từ đó đưa ra kết luận nghiệm cho phương trình.

+) Nếu k=0 thì ta có

B. Ví dụ minh họa

Câu 1: Phương trình |2x-5|=3 có nghiệm là:

A. x=4;x= - 1

B. x= - 4;x=1

C. x=4;x=1

D. x= - 4; x= - 1

Lời giải:

Vậy phương trình có nghiệm là x=4;x=1.

Câu 2: Giải phương trình .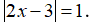

Lời giải:

Biến đổi tương đương phương trình:

Vậy, phương trình có hai nghiệm x=2 và x=1.

Câu 3: Giải phương trình:

Lời giải:

Điều kiện xác định của phương trình là x≠2.

Ta có thể lựa chọn một trong hai cách trình bày sau:

Cách 1: Biến đổi tương đương phương trình:

Vậy, phương trình có nghiệm x=0.

Cách 2: Biến đổi tương đương phương trình:

Vậy, phương trình có nghiệm x=0.

C. Bài tập tự luyện

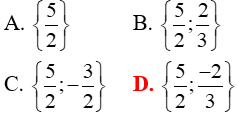
Câu 1: Phương trình 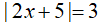có nghiệm là:

A. x=4;x= - 1

B. x= - 4;x=1

C. x=4;x=1

D. x= - 4; x= - 1

Câu 2: Phương trình nào sau đây vô nghiệm?

Câu 3: Hãy tìm các khẳng định đúng trong các khẳng định dưới đây?

Câu 4: Giải phương trình

Câu 5: Giải phương trình

Câu 6: Giải các phương trình sau:

Câu 7: Tìm m để phương trình 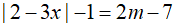có nghiệm duy nhất.

Dạng 2: Giải phương trình |A(x)| = |B(x)|

A. Phương pháp giải

Để giải phương trình chứa dấu giá trị tuyệt đối |A(x)| = |B(x)|, ta thực hiện theo các bước:

Bước 1: Đặt điều kiện để A(x) và B(x) xác định (nếu cần).

Bước 2: Khi đó:

=> nghiệm x.

Bước 3: Kiểm tra điều kiện, từ đó đưa ra kết luận nghiệm cho phương trình.

B. Ví dụ minh họa

Câu 1: Nghiệm nhỏ nhất của phương trình 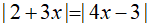là:

Lời giải:

Vậy nghiệm nhỏ nhất của phương trình là .

Câu 2: Giải các phương trình sau:

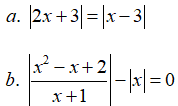
Lời giải:

a. Biến đổi tương đương phương trình:

Vậy, phương trình có hai nghiệm x=-6 và x=0.

b. Điều kiện xác định của phương trình là x≠1.

Biến đổi tương đương phương trình:

Vậy, phương trình có nghiệm là x=1.

Câu 3: Giải phương trình:

, với m là tham số.

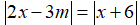
Lời giải:

Biến đổi tương đương phương trình:

Vậy, phương trình có hai nghiệm x=3m+6 và x=m-2.

C. Bài tập tự luyện

Câu 1: Nghiệm nhỏ nhất của phương trình 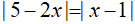là:

Câu 2: Cho hai phương trình

Hãy so sánh số nghiệm của hai phương trình trên.

Câu 3: Giải các phương trình sau:

Câu 4: Giải các phương trình sau:

Câu 5: Giải các phương trình sau:

Dạng 3: Giải phương trình |A(x)| = B(x)

A. Phương pháp giải

Để giải phương trình chứa dấu giá trị tuyệt đối |A(x)| = B(x), ta có thể lựa chọn một trong hai cách sau:

Cách 1: (Phá dấu trị tuyệt đối) Thực hiện theo các bước:

Bước 1: Đặt điều kiện để A(x) và B(x) xác định (nếu cần).

Bước 2: Xét hai trường hợp:

Trường hợp 1: Nếu 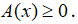. (1)

Phương trình có dạng:

=> nghiệm x và kiểm tra điều kiện (1).

Trường hợp 2: Nếu 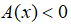(2)

Phương trình có dạng:

=> nghiệm x và kiểm tra điều kiện (2).

Bước 3: Kết luận nghiệm cho phương trình.

Cách 2: Thực hiện theo các bước:

Bước 1: Đặt điều kiện để A(x) và B(x) xác định (nếu cần) và .

Bước 2: Khi đó:

=> nghiệm x.

Bước 3: Kiểm tra điều kiện, từ đó đưa ra kết luận nghiệm cho phương trình.

B. Ví dụ minh họa

Câu 1: Tập nghiệm của phương trình 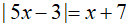là:

Lời giải:

Trường hợp 1:

Phương trình đã cho trở thành:

Trường hợp 2:

Phương trình đã cho trở thành:

Vậy tập nghiệm của phương trình là

Câu 2: Giải phương trình:

Lời giải:

Ta có thể lựa chọn một trong hai cách sau:

Cách 1: Xét hai trường hợp:

Trường hợp 1: Nếu 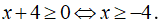(1)

Khi đó, phương trình có dạng:

Trường hợp 2: Nếu 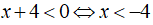(2)

Khi đó, phương trình có dạng:

Vậy, phương trình có nghiệm .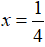

Cách 2: Viết lại phương trình dưới dạng:

Haylamdo biên soạn và sưu tầm điều kiện:

Khi đó, phương trình được biến đổi:

Vậy, phương trình có nghiệm .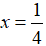

Câu 3: Giải các phương trình sau:

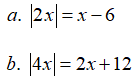
Lời giải:

a) Ta có:

Xét hai trường hợp:

Trường hợp 1: Nếu x ≥ 0 phương trình có dạng:

, không thỏa mãn điều kiện.

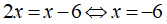
Trường hợp 2: Nếu x<0 phương trình có dạng:

, không thỏa mãn điều kiện.

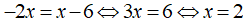
Vậy, phương trình vô nghiệm.

b) Với điều kiện:

(*)

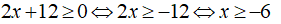
Khi đó, phương trình được biến đổi:

, thỏa mãn (*).

Vậy, phương trình có hai nghiệm x=6 và x=-2.

C. Bài tập tự luyện

Câu 1: Tập nghiệm của phương trình 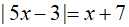là:

Caau2: Số nghiệm của phương trình 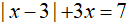là:

Câu 3: Giải các phương trình:

Câu 4: Giải các phương trình sau:

Câu 5: Giải các phương trình:

Câu 6: Giải các phương trình sau:

Câu 7: Giải các phương trình sau:

Câu 8: Giải phương trình sau bằng cách đặt ẩn phụ

Dạng 4: Giải phương trình |A(x)| + |B(x)| = C(x)

A. Phương pháp giải

Để giải phương trình chứa dấu giá trị tuyệt đối |A(x)| + |B(x)| = C(x):

- Chia các khoảng nghiệm để xác định dấu của biểu thức (lập bảng xét dấu).

- Căn cứ vào xét dấu, chia từng khoảng để giải phương trình (kiểm tra điều kiện tương ứng).

B. Ví dụ minh họa

Câu 1: Bỏ dấu giá trị tuyệt đối và rút gọn biểu thức:

Lời giải:

Nhận xét rằng:

Do đó, để bỏ được dấu giá trị tuyệt đối của C ta cần xét các trường hợp:

Trường hợp 1:

Trường hợp 2:

Trường hợp 3:

Câu 2: Giải phương trình

Lời giải:

Nhận xét rằng:

Trường hợp 1:

Khi đó phương trình trở thành:

Trường hợp 2:

Khi đó phương trình trở thành:

Trường hợp 3:

Khi đó phương trình trở thành:

Vậy phương trình có nghiệm duy nhất là .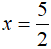

C. Bài tập tự luyện

Câu 1: Giải các phương trình sau:

Câu 2: Giải các phương trình sau:

Câu 3: Giải phương trình:

Câu 4: Cho phương trình 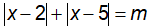(với m là tham số). Hãy cho biết với giá trị nào của m thì phương trình có hai nghiệm, vô số nghiệm, vô nghiệm?

Dạng 5: Giải phương trình |A(x)| + |B(x)| = |A(x) + B(x)|

A. Phương pháp giải

Để giải phương trình chứa dấu giá trị tuyệt đối |A(x)| + |B(x)| = |A(x) + B(x)|:

Ta nhận thấy vì 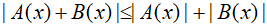nên phương trình tương đương với điều kiện xảy ra đẳng thức:

B. Ví dụ minh họa

Câu 1: Giải phương trình:

Lời giải:

Ta có:

Trường hợp 2:

Câu 2: Giải phương trình:

Lời giải:

Lập bảng xét giá trị tuyệt đối (hay bảng phá dấu GTTĐ):

C. Bài tập tự luyện

Câu 1: Giải phương trình:

Câu 2: Giải phương trình:

Câu 3: Giải các phương trình sau:

Câu 4: Giải phương trình: