Chứng minh hai đoạn thẳng bằng nhau trong hình bình hành
Chứng minh hai đoạn thẳng bằng nhau trong hình bình hành
Tài liệu Chứng minh hai đoạn thẳng bằng nhau trong hình bình hành Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải
1. Vẽ thêm hình bình hành bằng cách xác định một đoạn thẳng có trung điểm làm một đường chéo, sau đó chọn một trong hai giải pháp sau:
- Vẽ thêm đường chéo thứ hai.
- Kẻ thêm đường thẳng song song.
2. Áp dụng định lí đường trung bình của tam giác, định lý tổng các góc trong tam giác, tứ giác.
3. Áp dụng tính chất của hình bình hành:
- Hai cạnh song song và bằng nhau
- Hai góc đối bằng nhau
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
B. Ví dụ minh họa
Ví dụ 1. Cho tam giác ABC cân (AB = AC). Trên cạnh AB lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. Gọi I là giao điểm của BC và DE. Chứng minh DI = IE.
Giải
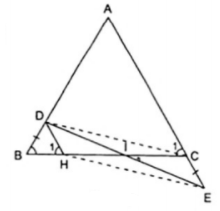
Kẻ DH//CE (H ∈ BC) (1)
Để chứng minh DI = IE ta chứng minh DCEH là hình bình hành.
Áp dụng tính chất về góc vào tam giác cân ABC và góc đồng vị của DH//CE, ta được:
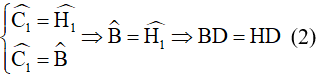
(vì trong một tam giác, đối diện với hai góc bằng nhau là hai cạnh bằng nhau).
Lại có BD = CE (3) theo giả thiết nên từ (2) và (3) suy ra DH = CE (4).
Từ (1) và (4) ta có tứ giác DCEH có hai cạnh đối song song và bằng nhau nên là hình bình hành.
Áp dụng tính chất về đường chéo vào hình bình hành DCEH thu được DI = IE.
Ví dụ 2. Cho tam giác ABC, trung tuyến AM. Gọi I là trung điểm của AM. D là giao điểm của BI với AC. Chứng minh rằng 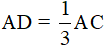 .
.
Giải
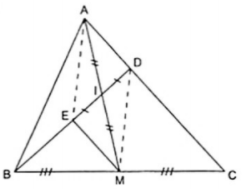
Do I là trung điểm của AM theo giả thiết nên chọn AM là một đường chéo. Vẽ thêm điểm E sao cho I là trung điểm của ED thì tứ giác ADME có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Áp dụng định nghĩa và tính chất về cạnh vào hình bình hành ADME, ta được
ME = AD (1) và ME//AD, ME//DC (2)
Lại có BM = MC. (3)
Từ (2) và (3) suy ra BE = ED theo định lí đường trung bình, lúc đó ME là đường trung bình của ΔBDC . Áp dụng định lí đường trung bình vào tam giác BDC, ta được:
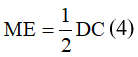
Từ (1) và (4) suy ra:
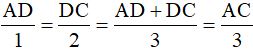
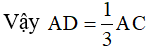
Ví dụ 3. Cho tam giác ABC. Qua D là trung điểm của cạnh BC, kẻ một đường thẳng vuông góc với đường phân giác của góc A nó cắt AB ở M và AC ở N. Chứng minh rằng BM = CN.
Giải
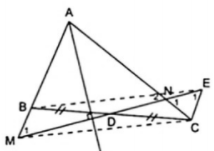
Do D là trung điểm của BC theo giả thiết nên chọn BC làm một đường chéo. Vẽ thêm điểm E sao cho D là trung điểm của ME thì tứ giác BMCE có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Áp dụng định nghĩa, tính chất về cạnh vào hình bình hành BMCE ta được BM//CE và
BM = CE. (1)
Mặt khác theo giả thiết trong tam giác AMN ta thấy MN vuông góc với tia phân giác của góc A nên tam giác AMN cân ở A.
Áp dụng tính chất về góc vào tam giác cân AMN, tính chất của hai góc đối đỉnh ở N và tính chất góc so le của BM//CE, ta được:
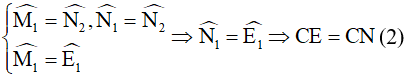
(vì trong một tam giác, đối diện với hai góc bằng nhau là hai cạnh bằng nhau).
Từ (1) và (2) suy ra BM = CN.
C. Bài tập vận dụng
Câu 1. Chọn câu sai. Cho ABCD là hình bình hành. Khi đó:
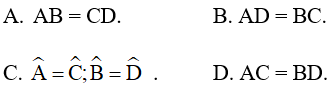
Câu 2. Hãy chọn câu đúng. Tứ giác ABCD là hình bình hành nếu:
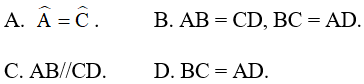
Câu 3. Hãy chọn câu đúng. Cho hình bình hành ABCD, gọi E là trung điểm của AB, F là trung điểm của CD. Khi đó:
Câu 4. Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D. Chọn câu sai.

Câu 5. Tỉ số độ dài hai cạnh của hình bình hành là 3:5. Còn chu vi của nó bằng 48cm. Độ dài hai cạnh kề của hình bình hành là:
A. 12cm và 20cm. B. 6cm và 10cm.
C. 3cm và 5cm. D. 9cm và 15cm .
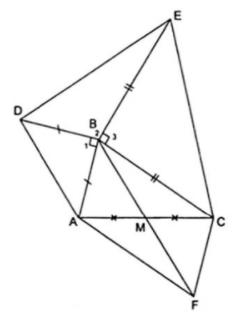
Câu 6. Vẽ ra phía ngoài tam giác ABC các tam giác ABD và BCE cùng vuông cân tại B, gọi M là trung điểm của AC. Chọn phương án đúng?
A. DE = 2BM.
B. DE = BM.
C. DE = 3BM.
D.DE = 4BM.
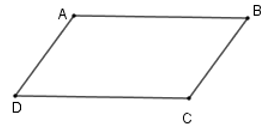
Câu 7. Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở E, F. Chọn khẳng định đúng.
A. DE = FE; FE > FB.
B. DE = FE = FB.
C. DE > FE; EF = FB.
D. DE > FE > FB.
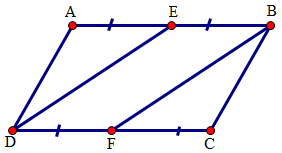
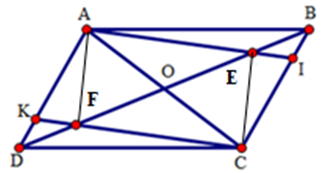
Câu 8. Cho hình bình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AD, BC. Đường chéo AC cắt BE, DF theo thứ tự ở K, I. Chọn khẳng định đúng nhất.
A. K, I lần lượt là trọng tâm ΔABD, ΔDBC .
B. AK = KI = IC.
C. Cả A, B đều đúng.
D. Cả A, B đều sai.
Câu 9. Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm E và F sao cho 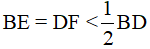 . Chọn khẳng định đúng.
. Chọn khẳng định đúng.
A. FA = CE.
B. FA < CE.
C. FA > CE.
D. Chưa kết luận được.
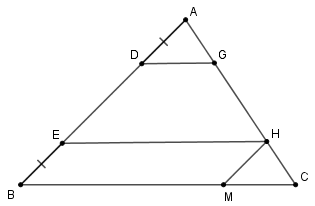
Câu 10. Cho tam giác ABC có BC = 6cm. Trên cạnh AB lấy các điểm D và E sao cho AD = BE. Qua D, E lần lượt vẽ các đường thẳng song song với BC, cắt AC theo thứ tự ở G và H. Tính tổng DG + EH.
A. 10 cm.
B. 4 cm.
C. 6 cm.
D. 8 cm.

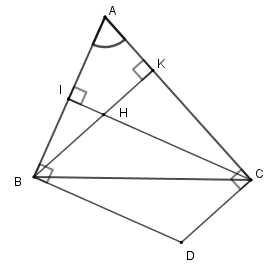
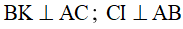 hay
hay 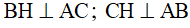 (vì H là trực tâm).
(vì H là trực tâm).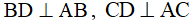 (giả thiết) nên BD//CH (cùng vuông với AB) và CD//BH (cùng vuông góc với AC)
(giả thiết) nên BD//CH (cùng vuông với AB) và CD//BH (cùng vuông góc với AC)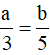
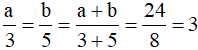
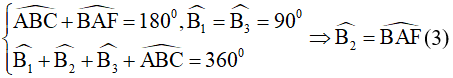
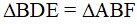 (c.g.c), do đó DE = BF.
(c.g.c), do đó DE = BF.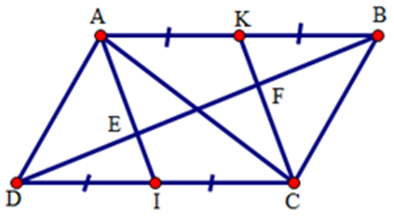
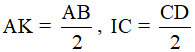 (gt) mà AB = CD (cạnh đối hình bình hành) nên AK = IC
(gt) mà AB = CD (cạnh đối hình bình hành) nên AK = IC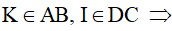 AK//IC.
AK//IC. EI//CF, KF//AE.
EI//CF, KF//AE.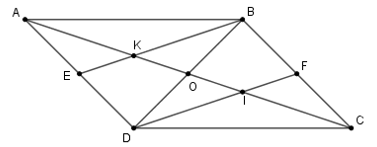
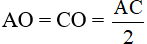
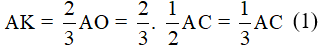
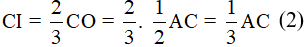
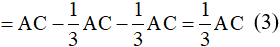
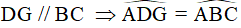 (hai góc ở vị trí đồng vị). (1)
(hai góc ở vị trí đồng vị). (1)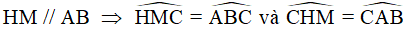 (hai góc ở vị trí đồng vị). (2)
(hai góc ở vị trí đồng vị). (2)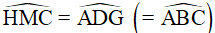 .
.