Cách chia đơn thức cho đơn thức cực hay, có lời giải chi tiết
Cách chia đơn thức cho đơn thức cực hay, có lời giải chi tiết
Tài liệu Cách chia đơn thức cho đơn thức cực hay, có lời giải chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải
1. Định nghĩa:
Haylamdo biên soạn và sưu tầm A và B là hai đơn thức,B ≠ 0. Ta nói A chia hết cho B nếu tìm được một đơn thức Q sao cho A = B. Q
Trong đó:
. A là đơn thức bị chia.
. B là đơn thức chia.
. Q là đơn thức thương (hay gọi là thương)
Kí hiệu: 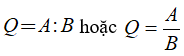
2. Quy tắc
Nhớ lại kiến thức cũ: Ở lớp 7 ta biết: Với 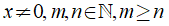
xm : xn = xm-n nếu m > n
xm : xn = 1 nếu m = n Và (xn)m = xn.m
Quy tắc:
Muốn chia đơn thức A cho đơn thức B (trường hợp A chia hết cho B) ta làm như sau:
+ Chia hệ số của đơn thức A cho hệ số của đơn thức B.
+ Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.
+ Nhân các kết quả vừa tìm được với nhau.
B. Ví dụ minh họa
Ví dụ 1. Tính (-4)13 : 410
A. – 64 B. 12 C. -12 D. 64
Lời giải
Ta có: (-4)13 : 410 = (-4)13 : (-4)10 = (-4)3 = -64
( vì (-4)10 = (-1.4)10 = (-1)10.410 = 1.410 = 410)
Chọn A.
Ví dụ 2. Tính 39x5 : 13x2
A.3x2 B. – 3x3 C. 3x3 D. -3x2
Lời giải
39x5 : 13x2 = (39 : 13).(x5 : x2) = 3x3
Chọn C.
Ví dụ 3. Tính 16x2y3 : (-4xy3)
A. – 4x.y B.4x2y C. – 4xy D. – 4x
Lời giải
16x2y3 : (-4xy3) = [16 : (-4)].(x2 : x)(y3 : y3)
= -4x2-1.y3-3 = -4x1.y0 = -4x
Chọn D.
Ví dụ 4. Tính (2x2y2)3 : (2xy2)
A.4x5y4 B. 2x2y C. 3x5y3 D. 3x3y3
Lời giải
(2x2y2)3 : (2xy2) = 8x6y6 : 2xy2
= (8 : 2).(x6 : x).(y6 : y2) = 4x5y4
Chọn A.
C. Bài tập trắc nghiệm
Câu 1. Tính 612 : (-6)8
A. 64 B. – 64 C. 62 D. - 62
612 : (-6)8 = 612 : 68 = 612-8 = 64
(-6)8 = (-1.68) = (-1)8.68 = 1.68 = 68
Chọn A
Câu 2. Tính (-8x6) : 2x3
A. 4x2 B. 4x3 C. – 4x3 D. -4x2
(-8x6) : 2x3 = (-8:2).(x6 : x3)
= -4x6-3 = -4x3
Chọn C.
Câu 3. Tính (2x3y4)3 : (x2y)4
A. 6xy7 B. 8xy7 C. 6x3y D. 8xy8
(2x3y4)3 : (x2y)4 = 8x9y12 : x8y4 = 8xy8
Chọn D.
Câu 4. Tính 12x5y7 : (-2x2y3)2
A. -6xy B. 3xy C. – 3xy D. 6xy
12x5y7 : (-2x2y3)2 = 12x5y7 : 4x4y6 = 3xy
Chọn B.
Câu 5. Tính (-8x2y5):(2xy)
A. – 4xy2 B. – 4xy5 C. – 4xy4 D. 4x2y5
(-8x2y5):(2xy) = -4xy4
Chọn C.
Câu 6. Tính (-2x3y5)3 : (2x3y5)2
A. 2x2y4 B. -2x3y5 C. - 2x2y4 D. – 2x3y5
(-2x3y5)3 : (22x3y5)2 = -8x9y15 : 4x6y10 = -2x3y5
Chọn D.
Câu 7. Tính (3x3y4)2 : (-xy2)3
A. - 9x2y2 B. – 9x3y2 C. 9x2y3 D. 3x2y3
(3x3y4)2 : (-xy2)3 = 9x6y8:(-x3y6) = -9x3y2
Chọn B.
Câu 8: Tính (-8x3y3):(-xy)3
A. 8 B. 8xy C. 8x D. 8y
(-8x3y3):(-xy)3 = (-8x3y3):(-x3y3) = 8
Chọn A.
Câu 9. Tính (-3x2y3)2 : 3xy2
A. – xy
B. – x2y2
C. - 3xy
D. 3x3y4
Ta có: (-3x2y3)2 : 3xy2 = 9x4y6 : 3xy2 = 3x3y4
Chọn D.
Câu 10. Tính x4y7 : (-2x2y)2
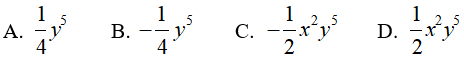
Ta có: 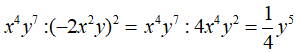
Chọn A .

