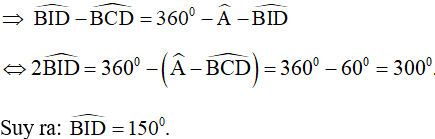Tính số đo góc trong tứ giác hay, chi tiết
Tính số đo góc trong tứ giác hay, chi tiết
Tài liệu Tính số đo góc trong tứ giác hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải.
Sử dụng:
- Tính chất về góc của một tam giác: Tổng các góc của một tam giác bằng 1800.
- Tính chất về góc của một tứ giác: Tổng các góc của một tứ giác bằng 3600.
- Khái niệm: Hai góc bù nhau là hai góc có tổng bằng 1800.
- Tính chất của dãy tỉ số bằng nhau:
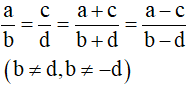
B. Ví dụ minh họa
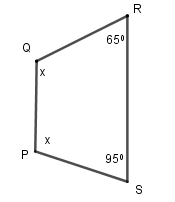
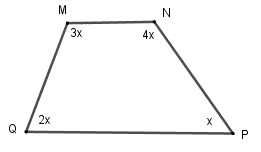
Ví dụ 1. Tìm x ở hình 4a và hình 4b.
a) b)
Giải
a) Áp dụng tính chất về tổng các góc cho tứ giác PQRS, ta được:
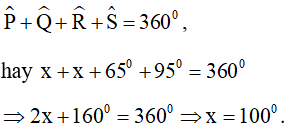
b) Áp dụng tính chất về tổng các góc cho tứ giác MNPQ ta được:
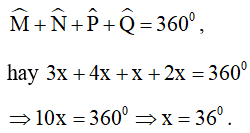
Ví dụ 2. Cho tứ giác ABCD có 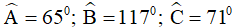 . Số đo góc ngoài tại đỉnh D bằng bao nhiêu?
. Số đo góc ngoài tại đỉnh D bằng bao nhiêu?
Giải
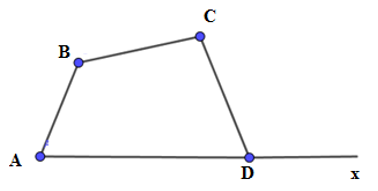
Kéo dài tia AD ta được tia Ax, suy ra 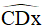 là góc ngoài đỉnh D.
là góc ngoài đỉnh D.
Áp dụng tính chất về tổng các góc cho tứ giác ABCD có:
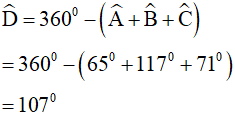
Ta thấy góc ngoài tại đỉnh D chính là góc 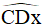
Vì 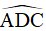 và
và 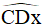 là hai góc kề bù nên
là hai góc kề bù nên
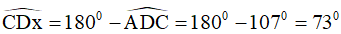
Ví dụ 3. Cho tứ giác MNPQ biết:
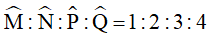
a) Tính các góc của tứ giác.
b) Gọi R là giao điểm của MQ với NP. Chứng minh rằng MN//PQ.
c) Tính các góc của tam giác PQR.
Giải
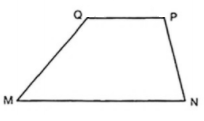
a) Viết lại giả thiết thành
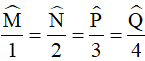
Áp dụng tính chất của dãy tỉ số bằng nhau và tính chất về tổng các góc vào tứ giác MNPQ ta có:
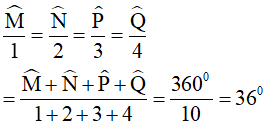
Vậy
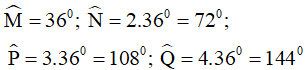
b)
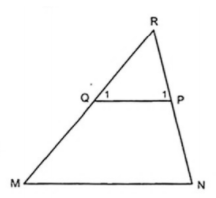
Vì 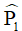 là góc ngoài của tứ giác MNPQ tại đỉnh P, nên:
là góc ngoài của tứ giác MNPQ tại đỉnh P, nên:
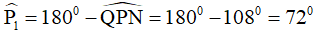
Do đó 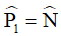 (cặp góc ở vị trí đồng vị bằng nhau).
(cặp góc ở vị trí đồng vị bằng nhau).
Vậy MN//PQ .
c)
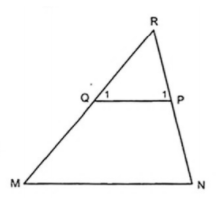
Theo câu b) thì 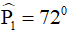 .
.
Ta có 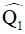 là góc ngoài của tứ giác MNPQ tại đỉnh Q.
là góc ngoài của tứ giác MNPQ tại đỉnh Q.
Nên
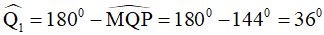
Áp dụng tính chất về tổng các góc vào tam giác PQR , ta có:
C. Bài tập vận dụng.
Câu 1. Hãy chọn câu sai.
A. Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kỳ cạnh nào của tứ giác.
B. Tổng các góc của một tứ giác bằng 1800 .
C. Tổng các góc của một tứ giác bằng 3600 .
D. Tứ giác ABCD là hình gồm đoạn thẳng AB, BC, CD, DA trong đó bất kỳ hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
Câu 2. Các góc của tứ giác có thể là:
A. 4 góc nhọn.
B. 4 góc tù.
C. 4 góc vuông.
D. 1 góc vuông, 3 góc nhọn.
Câu 3. Cho tứ giác ABCD có 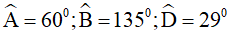 . Số đo góc C bằng:
. Số đo góc C bằng:

Câu 4. Cho tứ giác ABCD, trong đó 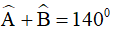 . Tổng
. Tổng 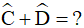
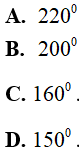
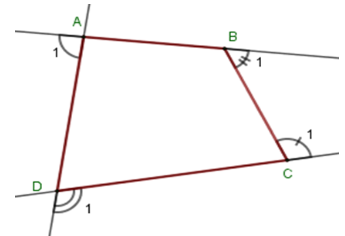
Câu 5. Cho tứ giác ABCD có 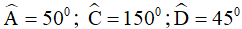 . Số đo góc ngoài tại đỉnh B bằng:
. Số đo góc ngoài tại đỉnh B bằng:
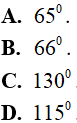
Câu 6. Cho tứ giác ABCD có 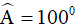 . Tổng số đo các góc ngoài đỉnh B, C, D bằng:
. Tổng số đo các góc ngoài đỉnh B, C, D bằng:
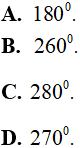
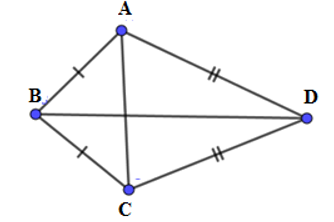
Câu 7. Tứ giác ABCD có AB = BC, CD = DA, 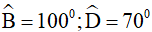 . Tính
. Tính 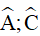 .
.
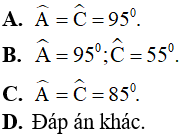
Câu 8. Cho tứ giác ABCD biết số đo của các góc 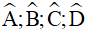 tỉ lệ thuận với 4; 3; 5; 6. Khi đó số đo các góc
tỉ lệ thuận với 4; 3; 5; 6. Khi đó số đo các góc 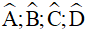 lần lượt là:
lần lượt là:
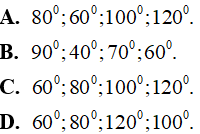
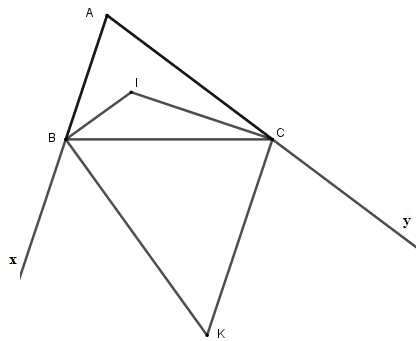
Câu 9. Tam giác ABC có 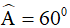 , các tia phân giác của góc B và C cắt nhau tại I. Các tia phân giác góc ngoài tại đỉnh B và C cắt nhau tại K. Tính các góc
, các tia phân giác của góc B và C cắt nhau tại I. Các tia phân giác góc ngoài tại đỉnh B và C cắt nhau tại K. Tính các góc 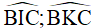
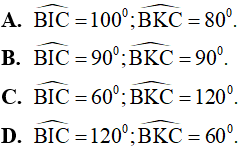
Câu 10. Cho tứ giác ABCD có 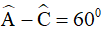 . Các tia phân giác của các góc B và D cắt nhau tại I. Tính số đo góc BID.
. Các tia phân giác của các góc B và D cắt nhau tại I. Tính số đo góc BID.


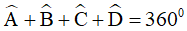 (định lý tổng các góc trong của một tứ giác)
(định lý tổng các góc trong của một tứ giác)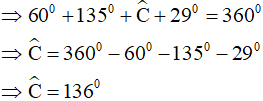
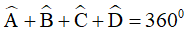 (định lý tổng các góc trong của một tứ giác)
(định lý tổng các góc trong của một tứ giác)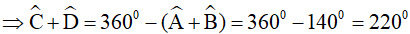
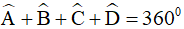 (định lý tổng các góc trong của một tứ giác)
(định lý tổng các góc trong của một tứ giác)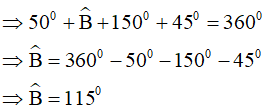
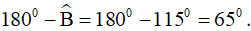
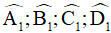 .
.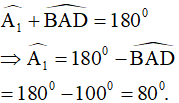
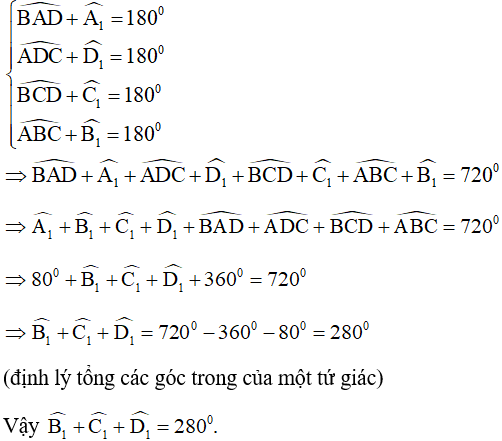
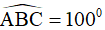 nên
nên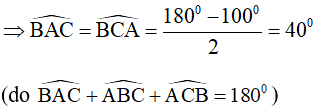
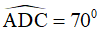 nên
nên 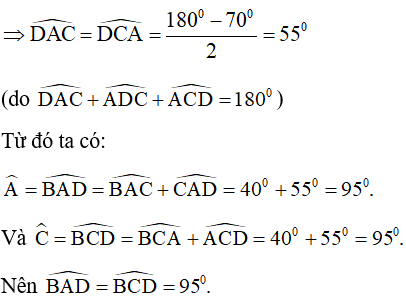
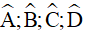 tỉ lệ thuận với 4; 3; 5; 6 nên ta có:
tỉ lệ thuận với 4; 3; 5; 6 nên ta có: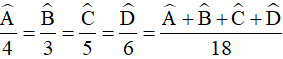
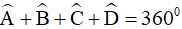 (tính chất tổng các góc trong của tứ giác) nên ta có
(tính chất tổng các góc trong của tứ giác) nên ta có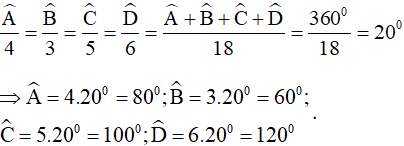
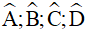 lần lượt là
lần lượt là 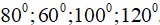
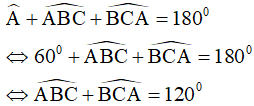
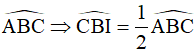
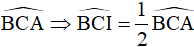
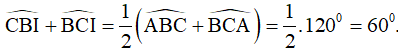
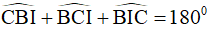 nên
nên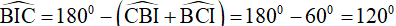
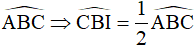
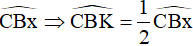
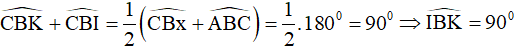
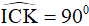
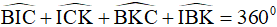 (tính chất tổng các góc trong của tứ giác)
(tính chất tổng các góc trong của tứ giác)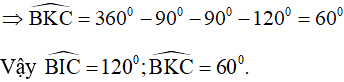
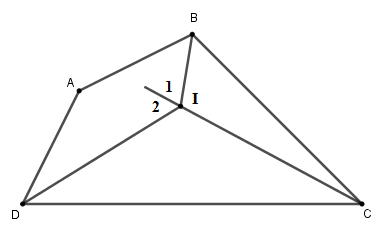
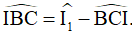 (tính chất góc ngoài)
(tính chất góc ngoài)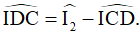 (tính chất góc ngoài)
(tính chất góc ngoài)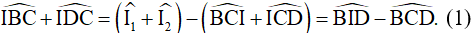
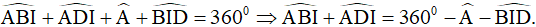
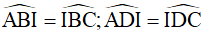
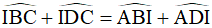 (3)
(3)