Công thức, cách tính góc của đa giác đều hay, chi tiết

Công thức, cách tính góc của đa giác đều hay, chi tiết

Tài liệu Công thức, cách tính góc của đa giác đều hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

Dạng bài: Tính góc của đa giác đều

A. Phương pháp giải

+) Sử dụng định nghĩa đa giác đều.

+) Mỗi góc của đa giác đều n cạnh bằng

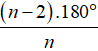
B. Ví dụ minh họa

Câu 1: Cho ABCDEF là hình lục giác đều. Hãy chọn câu sai?

A. ABCDEF có tâm đối xứng

B. Mỗi góc trong của nó là 120⁰

C. Tổng các góc trong của nó là 720⁰

D. Mỗi góc trong của nó là 150⁰

Giải.

A. Đúng

B. Đúng vì số đo góc trong của hình lục giác đều là:

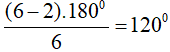
C. Đúng vì tổng số đo góc trong của lục giác đều là:

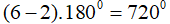
Vậy D sai

Câu 2: Tính số đo mỗi góc trong và ngoài của ngũ giác đều?

Lời giải:

Số đo góc trong của hình ngũ giác đều:

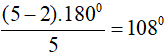
Vì góc trong và góc ngoài đa giác kề bù nên số đo góc ngoài của ngũ giác đều là:

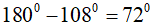
Câu 3: Một đa giác đều có tổng số đo tất cả các góc ngoài và một góc trong của đa giác là 468⁰. Hỏi đa giác đều có mấy cạnh?

Lời giải:

Gọi n là số cạnh của đa giác đều cần tìm (cạnh, )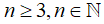

Mỗi góc trong của đa giác đều có số đo là:

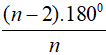
Tổng số đo các góc ngoài của một đa giác là 360⁰

Theo bài ra ta có phương trình:

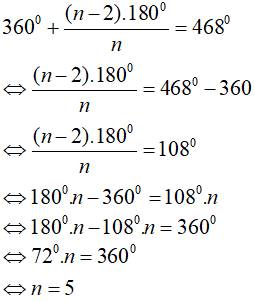
Vậy đa giác đều có 5 cạnh.

C. Bài tập tự luyện

Câu 1: Số đo mỗi góc của hình 9 cạnh đều là:

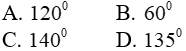
Câu 2: Cho đa giác đều có 14 cạnh. Tính:

a) Tổng số đo góc của đa giác đó

b) Số đo một góc của đa giác

c) Số đường chéo của đa giác.

Câu 3: Tính số đo mỗi góc trong của

a) Hình ngũ giác đều;

b) Hình lục giác đều;

c) Hình bát giác đều.

Câu 4: Cho ngũ giác đều ABCDE. Chứng minh rằng AC, AD chia góc A làm ba góc bằng nhau.

Câu 5: Muốn phủ kín mặt phẳng bởi những đa giác đều bằng nhau sao cho hai đa giác kề nhau thì có chung một cạnh. Hỏi các đa giác đều này có thể có nhiều nhất bao nhiêu cạnh?

Câu 6: Cho lục giác đều ABCDEF. Gọi M, N, P lần lượt là trung điểm của AB, CD, EF. Chứng minh ΔMNP đều.