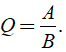Lý thuyết Chia đơn thức cho đơn thức hay, chi tiết

Lý thuyết Chia đơn thức cho đơn thức hay, chi tiết

Haylamdo biên soạn và sưu tầm Lý thuyết Chia đơn thức cho đơn thức hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Lý thuyết

1. Đơn thức chia cho đơn thức

Haylamdo biên soạn và sưu tầm A và B là hai đơn thức, B≠0. Ta nói A chia hết cho B nếu tìm được một đơn thức Q sao cho A = B.Q.

Trong đó:

   A là đơn thức bị chia.

   B là đơn thức chia.

   Q là đơn thức thương (hay gọi là thương)

Kí hiệu: Q = A : B hoặc

2. Quy tắc

Nhớ lại kiến thức cũ: Ở lớp 7 ta biết: Với x≠0; m, n ∈ N; m ≥ n thì:

x^m : xⁿ = x^{m - n}       nếu m>n

x^m : xⁿ = 1       nếu m=n

(xⁿ)^m = x^n.m

Quy tắc:

Muốn chia đơn thức A cho đơn thức B (trường hợp A chia hết cho B) ta làm như sau:

+ Chia hệ số của đơn thức A cho hệ số của đơn thức B.

+ Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.

+ Nhân các kết quả vừa tìm được với nhau.

Ví dụ: Thực hiện phép tính

a, ( - 2 )⁵:( - 2 )³.

b, ( xy² )⁴:( xy² )²

Hướng dẫn:

a) Ta có: ( - 2 )⁵:( - 2 )³ = ( - 2 )⁵ - 3 = ( - 2 )² = 4.

b) Ta có: ( xy² )⁴:( xy² )² = x⁴y⁸:x²y⁴ = x⁴ - 2.y⁸ - 4 = x²y⁴.

B. Bài tập tự luyện

Bài 1: Tính giá trị của các biểu thức sau

a) P = 12x⁴y²:(- 9xy² ) tại x= -3, y= 1,005.

b) Q = 3x⁴y³:2xy² tại x= 2, y= 1.

Hướng dẫn:

a) Ta có P = 12x⁴y²:( - 9xy² ) = 1/2 - 9x⁴ - 1y² - 2 = - 4/3x³

Haylamdo biên soạn và sưu tầm x= -3, y= 1,005 ta có P = - 4/3( - 3 )³ = 36.

Vậy P = 36

b) Ta có Q = 3x⁴y³:2xy² = 3/2x⁴ - 1y³ - 2 = 3/2x³y.

Haylamdo biên soạn và sưu tầm x= 2, y= 1 ta có Q = 3/2( 2 )³.1 = 12.

Vậy Q = 12

Bài 2: Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến y (x≠0; y≠0) với biểu thức đó là A = 2/3x²y³:( - 1/3xy ) + 2x( y - 1 )( y + 1 )

Hướng dẫn:

Ta có A = 2/3x²y³:( - 1/3xy ) + 2x( y - 1 )( y + 1 ) = - 2x² - 1y³ - 1 + 2x( y - 1 )( y + 1 )

= - 2xy² + 2x( y² - 1 ) = - 2xy² + 2xy² - 2x = - 2x

⇒ Giá trị của biểu thức A không phụ thuộc vào biến y