Vận dụng công thức tính diện tích để tính toán và chứng minh đẳng thức

Vận dụng công thức tính diện tích để tính toán và chứng minh đẳng thức

Tài liệu Vận dụng công thức tính diện tích để tính toán và chứng minh đẳng thức Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

Dạng bài: Vận dụng công thức tính diện tích để tính toán và chứng minh các yếu tố liên quan

A. Phương pháp giải

+) Vận dụng công thức diện tích các hình.

+) So sánh các yếu tố diện tích, cạnh, đường cao.

B. Ví dụ minh họa

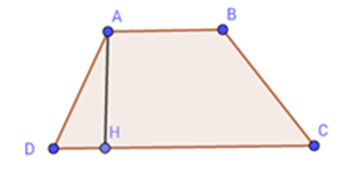
Câu 1: Cho hình thang ABCD (AB//CD), đường cao AH, AB = 4cm; CD = 8cm, diện tích hình thang là 54 cm². Tính độ dài AH?

Lời giải:

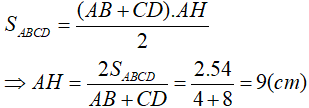
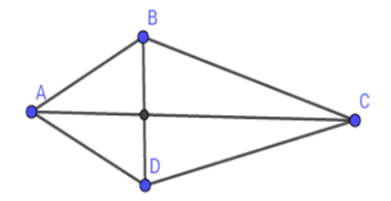
Câu 2: Cho tứ giác ABCD có đường chéo AC vuông góc với BD, diện tích của ABCD là 25cm² ; BD = 5cm. Tính độ dài đường cao chéo AC?

Lời giải:

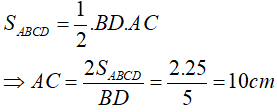
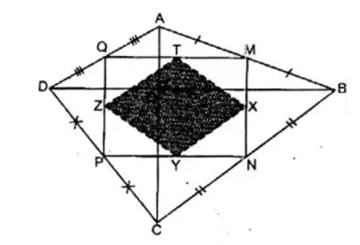
Câu 3: Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Biết AC = 6cm, BD = 8cm. Gọi M, N, P, Q theo thứ tự là trung điểm các cạnh AB, BC, CD, DA. Gọi X, Y, Z, T theo thứ tự là trung điểm các cạnh MN, NP, PQ, QM. Chứng minh rằng MNPQ là hình chữ nhật.

Giải.

Trong ΔABD ta có:

M là trung điểm của AB

Q là trung điểm của AD

nên MQ là đường trung bình của ΔABD.

⇒ MQ // BD và MQ = 1/2 BD (tính chất đường trung bình của tam giác) (1)

Trong ΔCBD ta có:

N là trung điểm của BC

P là trung điểm của CD

nên NP là đường trung bình của ΔCBD

⇒ NP // BD và NP = 1/2 BD (tính chất đường trung bình của tam giác) (2)

Từ (1) và (2) suy ra: MQ // NP và MQ = NP nên tứ giác MNPQ là hình bình hành

AC ⊥ BD (gt)

MQ // BD

Suy ra: AC ⊥ MQ

Trong ΔABC có MN là đường trung bình ⇒ MN // AC

Suy ra: MN ⊥ MQ hay (NMQ) = 90^o

Vậy tứ giác MNPQ là hình chữ nhật.

C. Bài tập tự luyện

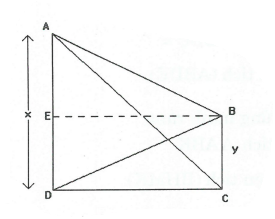
Câu 1: Hãy tính AE ở hình bên dưới. Biết rằng:

Tam giác ADC vuông cân tại D, EB//DC, AD//BC,

diện tích tam giác ADC = 8,

diện tích tam giác BDC = 3.

Câu 2: Cho hình bình hành ABCD có AB = 6cm, AD = 5cm. Kẻ AH vuông góc với CD, kẻ AK vuông góc với BC. Biết AH = 4cm. Tính AK.

Câu 3: Cho hình bình hành ABCD có các điểm E, F, G, H lần lượt thuộc AB, BC, DA sao cho EG không song song với AD. Biết rằng diện tích EFGH bằng 1/2 diện tích ABCD. Chứng minh HF//CD.

Câu 4: Cho hình bình hành ABCD, trên BC lấy điểm I và trên AB lấy điểm K sao cho AI = CK. Gọi O là giao điểm của AI và CK. Chứng minh OD là phân giác của góc AOC.

Câu 5: Cho hình thang ABCD (AB // CD). Gọi M, N lần lượt là trung điểm của AB, CD. Một đường thẳng song song với hai đáy cắt AD ở E, MN ở I, BC ở F. Chứng minh IE = IF.

Câu 6: Cho hình vuông ABCD có độ dài cạnh 6cm. Trên AB, CD lần lượt lấy M, N sao cho AM = CN. Tìm vị trí của M để diện tích tứ giác AMCN bằng 1/9 diện tích tứ giác ABCD.

Câu 7: Cho ΔABC vuông cân, có cạnh huyền BC = a. Gọi D là trung điểm của AB. Điểm E di chuyển trên cạnh AC. Gọi H, K thứ tự là chân đường vuông góc kẻ từ D, E đến BC. Tính diện tích lớn nhất của hình thang DEKH. Khi đó hình thang trở thành hình gì?