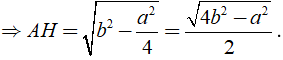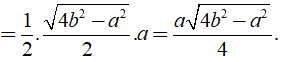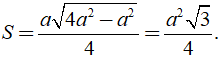Lý thuyết Diện tích tam giác hay, chi tiết

Lý thuyết Diện tích tam giác hay, chi tiết

Haylamdo biên soạn và sưu tầm Lý thuyết Diện tích tam giác hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Lý thuyết

1. Định lý

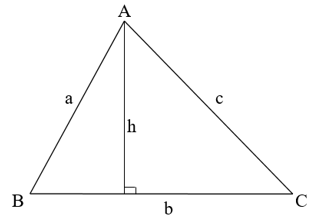
Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.

Ta có: S = 1/2b.h.

Ví dụ: Cho tam giác Δ ABC có độ dài đường cao h = 4 cm, đáy BC = 5 cm. Tính diện tích Δ ABC ?

Hướng dẫn:

Diện tích của tam giác Δ ABC là S_ABC = 1/2BC.h = 1/24.5 = 10 ( cm² ).

2. Hệ quả

Nếu Δ ABC vuông (áp dụng với hình bên trên) thì diện tích của tam giác bằng một nửa của tích hai cạnh góc vuông.

Tổng quát : S = 1/2a.c (áp dụng với kí hiệu ở hình trên).

Ví dụ: Cho Δ ABC vuông tại A có cạnh AB = 3 cm;AC = 4 cm. Tính diện tích của tam giác Δ ABC ?

Hướng dẫn:

Diện tích của tam giác ABC là S_ABC = 1/2AB.AC = 1/2.3.4 = 6( cm² )

B. Bài tập tự luyện

Bài 1: Tính diện tích của một tam giác cân có cạnh đáy là a, cạnh bên bằng b. Từ đó hãy tính diện tích của một tam giác đều có cạnh bằng a.

Hướng dẫn:

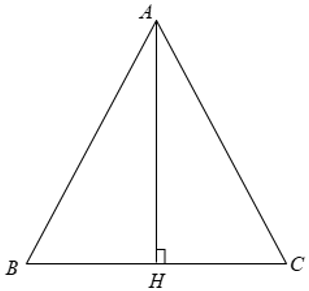
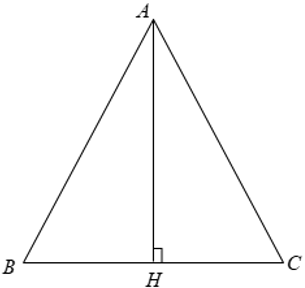
Xét Δ ABC cân tại A có AB = AC = b, BC = a.

Từ A kẻ AH ⊥ BC.

Ta có BH = HC = 1/2BC = a/2

Khi đó ta có: S_ABC = 1/2AH.BC = 1/2.a.AH

Áp dụng định lý Py – to – go ta có:

AC² = AH² + HC² ⇒ AH = √ (AC² - HC²) .

Khi đó S_ABC = 1/2AH.BC

Do đó diện tích của tam giác đều các cạnh bằng a là

Bài 2: Cho Δ ABC cân tại A có BC = 30( cm ), đường cao AH = 20 ( cm ). Tính đường cao ứng với cạnh bên của tam giác cân đó.

Hướng dẫn:

Xét Δ ABC cân tại A có BC = 30( cm )

⇒ BH = CH = 15( cm ).

Áp dụng đinh lý Py – ta – go ta có:

AB = √ (AH² + HB²) = √ (20² + 15²) = 25( cm )

Kẻ BK ⊥ AC, giờ ta phải tính BK = ?

Ta có : S_ABC = 1/2AH.BC = 1/2.20.30 = 300 ( cm² )

Mặt khác S_ABC = 1/2BK.AC = 1/2.BK.25

Do đó, ta có 1/2BK.25 = 300 ⇔ BK = (2.300)/25 = 24( cm ).