Những hằng đẳng thức đáng nhớ đầy đủ, chi tiết
Những hằng đẳng thức đáng nhớ đầy đủ, chi tiết
Haylamdo biên soạn và sưu tầm Những hằng đẳng thức đáng nhớ đầy đủ, chi tiết Toán lớp 8 tổng hợp bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm bài tập từ đó đạt điểm cao trong bài thi môn Toán lớp 8.

A. Lý thuyết
1. Bình phương của một tổng
Haylamdo biên soạn và sưu tầm A, B là các biểu thức tùy ý, ta có: ( A + B )2 = A2 + 2AB + B2.
Ví dụ:
a) Tính ( a + 3 )2.
b) Viết biểu thức x2 + 4x + 4 dưới dạng bình phương của một tổng.
Hướng dẫn:
a) Ta có: ( a + 3 )2 = a2 + 2.a.3 + 32 = a2 + 6a + 9.
b) Ta có x2 + 4x + 4 = x2 + 2.x.2 + 22 = ( x + 2 )2.
2. Bình phương của một hiệu
Haylamdo biên soạn và sưu tầm A, B là các biểu thức tùy ý, ta có: ( A - B )2 = A2 - 2AB + B2.
Ví dụ:
a) Tính ( 5x -y )2
b) Viết biểu thức 4x2 - 4x + 1 dưới dạng bình phương của một hiệu
Hướng dẫn:
p>a) Ta có ( 5x -y )2 = ( 5x )2 - 2.5x.y + ( y )2 = 25x2 - 10xy + y2.b) Ta có 4x2 - 4x + 1 = ( 2x )2 - 2.2x.1 + 1 = ( 2x - 1 )2.
3. Hiệu hai bình phương
Haylamdo biên soạn và sưu tầm A, B là các biểu thức tùy ý, ta có: A2 - B2 = ( A - B )( A + B ).
Ví dụ:
a) Tính ( x - 2 )( x + 2 ).
b) Tính 56.64
Hướng dẫn:
a) Ta có: ( x - 2 )( x + 2 ) = ( x )2 - 22 = x2 - 4.
b) Ta có: 56.64 = ( 60 - 4 )( 60 + 4 ) = 602 - 42 = 3600 - 16 = 3584.
4. Lập phương của một tổng
Haylamdo biên soạn và sưu tầm A, B là các biểu thức tùy ý, ta có: ( A + B )3 = A3 + 3A2B + 3AB2 + B3.
Ví dụ:
a) Tính ( x + 2 )3.
b) Viết biểu thức x3 + 3x2 + 3x + 1 dưới dạng lập phương của một tổng.
Hướng dẫn:
a) Ta có ( x + 2 )3 = x3 + 3.x2.2 + 3x.22 + 23 = x3 + 6x2 + 12x + 8.
b) Ta có x3 + 3x2 + 3x + 1 = x3 + 3x2.1 + 3x.12 + 13 = ( x + 1 )3.
5. Lập phương của một hiệu.
Haylamdo biên soạn và sưu tầm A, B là các biểu thức tùy ý, ta có: ( A - B )3 = A3 - 3A2B + 3AB2 - B3.
Ví dụ :
a) Tính ( 2x - 1 )3.
b) Viết biểu thức x3 - 6x2y + 12xy2 - 8y3 dưới dạng lập phương của một hiệu.
Hướng dẫn:
a) Ta có: ( 2x - 1 )3 = ( 2x )3 - 3.( 2x )2.1 + 3( 2x ).12 - 13 = 8x3 - 12x2 + 6x - 1
b) Ta có : x3 - 6x2y + 12xy2 - 8y3 = ( x )3 - 3.x2.2y + 3.x.( 2y )2 - ( 2y )3 = ( x - 2y )3
6. Tổng hai lập phương
Haylamdo biên soạn và sưu tầm A, B là các biểu thức tùy ý, ta có: A3 + B3 = ( A + B )( A2 - AB + B2 ).
Chú ý: Ta quy ước A2 - AB + B2 là bình phương thiếu của hiệu A - B.
Ví dụ:
a) Tính 33 + 43.
b) Viết biểu thức ( x + 1 )( x2 - x + 1 ) dưới dạng tổng hai lập phương.
Hướng dẫn:
a) Ta có: 33 + 43 = ( 3 + 4 )( 32 - 3.4 + 42 ) = 7.13 = 91.
b) Ta có: ( x + 1 )( x2 - x + 1 ) = x3 + 13 = x3 + 1.
7. Hiệu hai lập phương
Haylamdo biên soạn và sưu tầm A, B là các biểu thức tùy ý, ta có: A3 - B3 = ( A - B )( A2 + AB + B2 ).
Chú ý: Ta quy ước A2 + AB + B2 là bình phương thiếu của tổng A + B.
Ví dụ:
a) Tính 63 - 43.
b) Viết biểu thức ( x - 2y )( x2 + 2xy + 4y2 ) dưới dạng hiệu hai lập phương
Hướng dẫn:
a) Ta có: 63 - 43 = ( 6 - 4 )( 62 + 6.4 + 42 ) = 2.76 = 152.
b) Ta có : ( x - 2y )( x2 + 2xy + 4y2 ) = ( x )3 - ( 2y )3 = x3 - 8y3.
B. Bài tập tự luyện
Bài 1: Tính giá trị của các biểu thức sau:
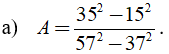
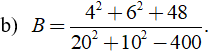
Hướng dẫn:
a) Ta có: 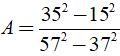
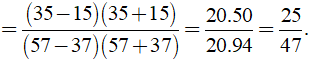
(áp dụng hằng đẳng thức a2 - b2 = ( a + b )( a - b ) )
Vậy A = 25/47.
b) Ta có 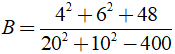
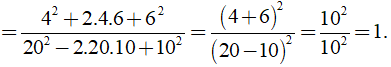
(áp dụng hằng đẳng thức ( a + b )2 = a2 + 2ab + b2; ( a - b )2 = a2 - 2ab + b2 )
Vậy B = 1.
Bài 2: Tìm x biết
a) ( x - 3 )( x2 + 3x + 9 ) + x( x + 2 )( 2 - x ) = 0.
b) ( x + 1 )3 - ( x - 1 )3 - 6( x - 1 )2 = - 10.
Hướng dẫn:
a) Áp dụng các hằng đẳng thức ( a - b )( a2 + ab + b2 ) = a3 - b3.
( a - b )( a + b ) = a2 - b2.
Khi đó ta có ( x - 3 )( x2 + 3x + 9 ) + x( x + 2 )( 2 - x ) = 0.
⇔ x3 - 33 + x( 22 - x2 ) = 0 ⇔ x3 - 27 + x( 4 - x2 ) = 0
⇔ x3 - x3 + 4x - 27 = 0
⇔ 4x - 27 = 0 ⇔ x = 27/4.
Vậy giá trị x cần tìm là x= 27/4 .
b) Áp dụng hằng đẳng thức ( a - b )3 = a3 - 3a2b + 3ab2 - b3
( a + b )3 = a3 + 3a2b + 3ab2 + b3
( a - b )2 = a2 - 2ab + b2
Khi đó ta có: ( x + 1 )3 - ( x - 1 )3 - 6( x - 1 )2 = - 10.
⇔ ( x3 + 3x2 + 3x + 1 ) - ( x3 - 3x2 + 3x - 1 ) - 6( x2 - 2x + 1 ) = - 10
⇔ 6x2 + 2 - 6x2 + 12x - 6 = - 10
⇔ 12x = - 6 ⇔ x = - 1/2.
Vậy giá trị x cần tìm là x= - 1/2

