Giải bài toán tỉ số diện tích tam giác bằng tính chất đường phân giác

Giải bài toán tỉ số diện tích tam giác bằng tính chất đường phân giác

Tài liệu Giải bài toán tỉ số diện tích tam giác bằng tính chất đường phân giác Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

Dạng bài: Bài toán liên quan đến tỉ số diện tích tam giác

A. Phương pháp giải

+) Vận dụng công thức tính diện tích tam giác và tính chất đường phân giác của tam giác.

B. Ví dụ minh họa

Câu 1: Cho tam giác ABC vuông tại A có AB = 12cm, AC = 16cm. Tia phân giác của góc A cắt BC tại D.

a) Tính tỉ số diện tích hai tam giác ABD và ACD.

b) Tính độ dài cạnh BC của tam giác.

c) Tính độ dài các đoạn thẳng BD và CD.

d) Tính chiều cao AH của tam giác.

Lời giải:

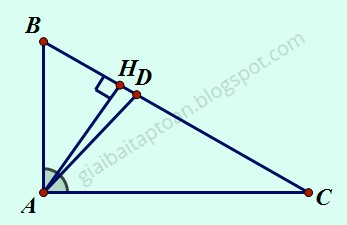
a) Ta có AD là tia phân giác góc A nên:

b) Áp dụng định lý Pi – ta – go trong tam giác vuông ABC, ta có:

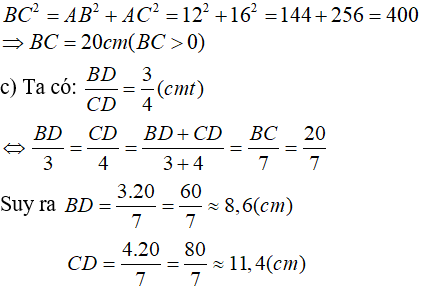
Câu 2: Cho ∆ABC với đường trung tuyến AM và đường phân giác AD. Tính diện tích ∆ADM, biết AB = m, AC = n (n > m) và diện tích của ∆ABC là S.

b. Cho n = 7cm, m = 3cm, hỏi diện tích ∆ADM chiếm bao nhiêu phần trăm diện tích ∆ABC?

Lời giải:

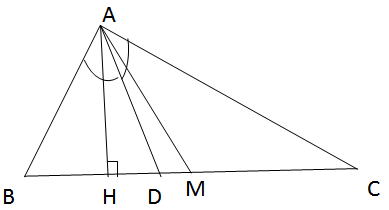
a. Kẻ đường cao AH của ∆ABC (H∈BC), ta có:

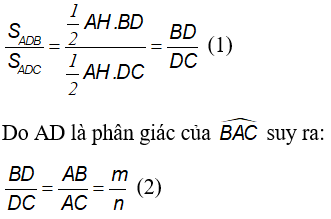
Do n > m (gt) nên DC > DB. Suy ra, D nằm giữa B và M.

Từ (1) và (2) suy ra:

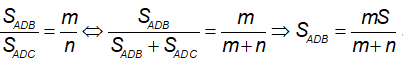
Do D nằm giữa B và M nên S_ADM + S_ADB = S_AMB (3)

Lại có:

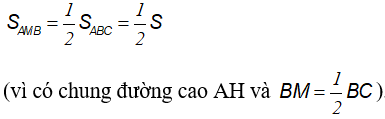
Từ (3) suy ra:

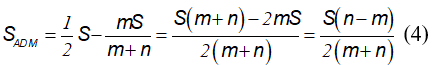
b. Thay n = 7cm, m = 3cm vào (4), ta được:

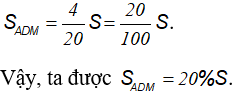
C. Bài tập tự luyện

Câu 1: Cho ∆ABC có AB = 4cm, AC = 6cm và AD là đường phân giác. Tính tỉ số diện tích của ∆ABD và ∆DAC.

Câu 2: Cho tam giác ABC có tỉ số giữa hai cạnh chung đỉnh A là 3:2. Vẽ đường trung tuyến AM và đường phân giác AK. Tính tỉ số diện tích của hai tam giác AKM và AKB.