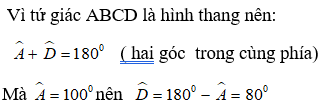Bài tập Hình thang chọn lọc, có đáp án
Bài tập Hình thang chọn lọc, có đáp án
Haylamdo biên soạn và sưu tầm Bài tập Hình thang chọn lọc, có đáp án Toán lớp 8 tổng hợp bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm bài tập từ đó đạt điểm cao trong bài thi môn Toán lớp 8.
I. Bài tập trắc nghiệm
Bài 1: Chọn câu đúng trong các câu sau:
A. Hình thang có ba góc tù, một góc nhọn.
B. Hình thang có ba góc vuông, một góc nhọn.
C. Hình thang có ba góc nhọn, một góc tù.
D. Hình thanh có nhiều nhất hai góc nhọn và nhiều nhất hai góc tù.
Ta có tổng các góc của hình thang bằng 3600.
+ Hình thang có ba góc tù, một góc nhọn.
Ví dụ: Hình thang có 3 góc tù là 1000,1200,1350 và 1 góc nhọn là 600.
⇒ Tổng 4 góc của hình thang bằng 1000 + 1200 + 1350 + 600 = 4150 > 3600
⇒ Không tồn tại hình thang có ba góc tù, một góc nhọn. ⇒ Đáp án A sai
+ Hình thang có ba góc vuông, một góc nhọn.
Ví dụ: Hình thang có 3 góc bằng 900 và một góc nhọn bằng 650.
⇒ Tổng 4 góc của hình thang bằng 900 + 900 + 900 + 650 = 3350 < 3600
⇒ Không tồn tại hình thang ba góc vuông, một góc nhọn. ⇒ Đáp án B sai.
+ Hình thang có ba góc nhọn, một góc tù.
Ví dụ: Hình thang có ba góc nhọn là 450,750,800, một góc tù là 1600
⇒ Tổng 4 góc của hình thang bằng 450 + 750 + 800 + 1600 = 3600
⇒ Tồn tại Hình thang có ba góc nhọn, một góc tù. ⇒ Đáp án C đúng
⇒ Hình thang có nhiều nhất là 3 góc nhọn. ⇒ Đáp án D sai.
Chọn đáp án C.
Bài 2: Một hình thang có một cặp góc đối là 1250 và 750, cặp góc đối còn lại của hình thang đó là ?
A. 1050,550 B. 1050,450
C. 1150,550 D. 1150,650
Tổng bốn góc của hình thang bằng 3600.
Theo giả thiết ta có một cặp góc đối là 1250 và 750
⇒ Tổng số đo góc của cặp góc đối còn lại là 1600.
Xét đáp án ta có cặp 1050,550 thỏa mãn.
Chọn đáp án A.
Bài 3: Hình thang ABCD có Cˆ + Dˆ = 1500. Khi đó Aˆ + Bˆ = ?
A. 2200 B. 2100
C. 2000 D. 1900
Tổng bốn góc của hình thang bằng 3600.
Khi đó ta có: Aˆ + Bˆ + Cˆ + Dˆ = 3600 ⇒ Aˆ + Bˆ = 3600 - ( Cˆ + Dˆ )
⇒ Aˆ + Bˆ = 3600 - 1500 = 2100.
Chọn đáp án B.
Bài 4: Cho hình thang ABCD trong đó có Aˆ = 1200, Bˆ = 600, Dˆ = 1350 thì số đo của góc Cˆ = ?
A. 550 B. 450
C. 500 D. 600
Tổng bốn góc của hình thang bằng 3600.
Khi đó ta có: Aˆ + Bˆ + Cˆ + Dˆ = 3600 ⇒ Cˆ = 3600 - ( Aˆ + Bˆ + Dˆ )
⇒ Cˆ = 3600 - ( 1200 + 600 + 1350 ) = 450.
Chọn đáp án B.
Bài 5: Cho hình thang ABCD có AB // CD. Biết Aˆ = 100o, tính Dˆ
A. 80o B. 100o
C. 120o D. 50o
Chọn đáp án A
Bài 6: Cho hình thang ABCD có AB // CD và Aˆ = 120o, Bˆ = 120o. Tính Cˆ, Dˆ
Chọn đáp án A
Bài 7: Cho hình thang vuông ABCD vuông tại A và D. Biết AD = 3 cm và CD = 4cm. Tính AC?
A. 3cm B. 4cm
C. 3,5cm D. 5cm
Do tứ giác ABCD là hình thang vuông nên Dˆ = 90o
Suy ra, tam giác ADC là tam giác vuông tại D.
Áp dụng đinh lí Py ta go vào tam giác vuông ACD ta có:
AC2 = AD2 + DC2 = 322 + 42 = 25
Suy ra: AC = 5cm
Chọn đáp án D
Bài 8: Cho tứ giác lồi ABCD có AB // CD và AD = 6cm; DC = 8cm và AC = 10cm. Tìm khẳng định sai ?
A. Tam giác ADC vuông tại D.
B. Tứ giác ABCD là hình thang
C. Tứ giác ABCD là hình thang vuông có Dˆ = 90o
D. Tứ giác ABCD là hình thang vuông có Bˆ = 90o
Tứ giác ABCD có AB // CD nên tứ giác ABCD là hình thang có 2 đáy là AB và CD.
Xét tam giác ACD có: AD2 + CD2 = AC2 (62 + 82 = 102 = 100)
Suy ra: tam giác ADC là tam giác vuông tại D.
Do đó: Dˆ = 90o
Suy ra: Tứ giác ABCD là hình thang vuông có Dˆ = 90o
Vậy khẳng định D sai
Chọn đáp án D
Bài 9: Cho hình thang ABCD có AB // CD và Aˆ = 2Dˆ. Tính góc A?
A. 60o B. 120o
C. 90o D. 80o
Chọn đáp án B
Bài 10: Cho hình thang ABCD có AB // CD và Cˆ - Bˆ = 30o . Tính góc C?
A. 105o B. 90o
C. 75o D. 60o
Chọn đáp án A
