Cách giải phương trình tích cực hay, có đáp án
Cách giải phương trình tích cực hay, có đáp án
Tài liệu Cách giải phương trình tích cực hay, có đáp án Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải
Để giải phương trình tích, ta áp dụng công thức: A(x).B(x) = 0 ⇔ A(x) = 0 hoặc B(x) = 0
Ta giải hai phương trình A(x) = 0 và B(x) = 0, rồi lấy tất cả các nghiệm của chúng.
B. Ví dụ minh họa
Ví dụ 1: Giải các phương trình sau:
a) (x + 1)(3x – 3) = 0
b) (2x + 4)(x + 3) = 0
Hướng dẫn giải:
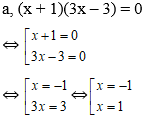
Vậy phương trình đã cho có tập nghiệm là S ={-1; 1}
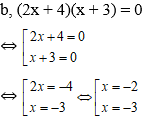
Vậy phương trình đã cho có tập nghiệm là S ={-2; -3}
Ví dụ 2: Giải các phương trình sau:
a) (4x - 10)(x2 + 2) = 0
b) (x - 4)(15 - 3x) = 0
Hướng dẫn giải:

Ví dụ 3: Giải các phương trình sau:
a, (x - 5)(3 - 2x)(3x + 4) = 0
b, (x – 1)(x +2)(x - 3)(x + 4)(x – 5) = 0
Hướng dẫn giải:

Ví dụ 4: Giải các phương trình sau:
a, (x – 2)(3x + 5) = (2x - 4)(x +1)
b, (2x - 1)2 = 49
Hướng dẫn giải:
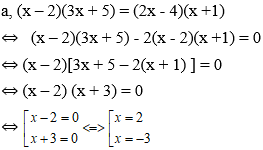
Vậy phương trình đã cho có tập nghiệm là S ={-3; 2}
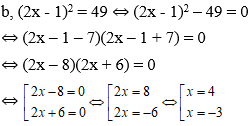
Vậy phương trình đã cho có tập nghiệm là S ={-3; 4}
C. Bài tập vận dụng
Bài 1: Nghiệm của phương trình (x – 3)(2x + 5) = 0 là
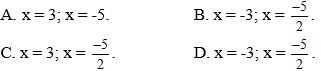
Đáp án: C
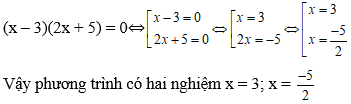
Bài 2: Tập nghiệm của phương trình (5x – 10)(8 - 2x) = 0 là
A. S = { 2; - 5}
B. S = { -2; 5}
C. S = { 2; - 4}
D. S = { 2; 4}.
Đáp án: D
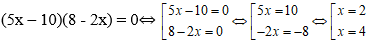
Vậy phương trình có tập nghiệm S = { 2; 4}.
Bài 3: Tập nghiệm của phương trình (7x – 3)(x2 + 4) = 0 là

Đáp án: A
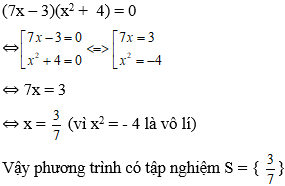
Bài 4: Phương trình (9 – 3x)(15 + 3x) = 0 có tập nghiệm là:
A. S= { 3}
B. S = { 3; 5}
C. S = { -5; 3}
D. { -5; - 3}
Đáp án: C
(9 – 3x)(15 + 3x) = 0 ⇔ 9 - 3x = 0 hoặc 15+ 3x = 0 ⇔ -3x = -9 hoặc 3x = -15
⇔ x = 3 hoặc x = -5
Vậy phương trình có hai nghiệm x = - 5 và x = 3.
Bài 5: Tập nghiệm của phương trình (2x + 5)(x – 4) = (x – 5)(4 – x) là
A. S = { -2; 4; 5}
B. S = { 0; 4}
C. S = { 0; 5 }
D. S = { 4; 5}
Đáp án: B
Ta có: (2x + 5)(x – 4) = (x – 5)(4 – x)
⇔ (2x + 5)(x – 4) - (x – 5)(4 – x) = 0
⇔ (2x + 5)(x – 4) + (x – 5)(x – 4) = 0
⇔ (x – 4)(2x + 5 + x – 5) = 0⇔ (x – 4)3x = 0
⇔ 3x = 0 hoặc x – 4 = 0 ⇔ x = 0 hoặc x = 4
Vậy phương trình có hai nghiệm x = 0 và x = 4.
Bài 6: Giải các phương trình sau:
a, (x – 3)(2x + 1) = 0
b, (3x + 4)(5 – x) = 0
Hướng dẫn giải:
a, (x – 3)(2x + 1) = 0 ⇔ x – 3 = 0 hoặc 2x + 1 = 0
⇔ x = 3 hoặc 2x = -1 ⇔ x = 3 hoặc x = -1/2
Vậy phương trình có hai nghiệm x = -1/2 và x = 3.
b, (3x + 4)(5 – x) = 0 ⇔ 3x +4 = 0 hoặc 5 - x = 0 ⇔ 3x = -4 hoặc –x = -5
⇔ x = -4/3 hoặc x = 5
Vậy phương trình có hai nghiệm x = -4/3 và x = 5.
Bài 7: Giải các phương trình sau:
a, (2x - 1)(x – 3)(3x + 7) = 0
b, x2 – 9 = (x - 3)(2x – 3)
Hướng dẫn giải:

Bài 8: Giải các phương trình sau:
a, 16x2 – 8x + 1 = 4(x + 3)(4x – 1)
b, (x + 2)2 = 9(x2 – 4x + 4)
Hướng dẫn giải:

Bài 9: Giải các phương trình sau:
a,(9x2 – 4)(x + 1) = (3x + 2)(x2 - 1)
b, x4 + x3 + x + 1 = 0
Hướng dẫn giải:
a, (9x2 – 4)(x + 1) = (3x + 2)(x2 - 1)
⇔ (3x – 2)(3x + 2)(x + 1) - (3x + 2)(x - 1)(x + 1) = 0
⇔(3x+ 2)(x + 1)(3x – 2 – x + 1) = 0
⇔ (3x + 2)(x + 1)(2x – 1) = 0

b, x4 + x3 + x + 1 = 0 ⇔ (x4 + x3) + (x + 1) = 0
⇔ x3 (x + 1) + (x + 1) = 0 ⇔ (x + 1)(x3 + 1) = 0
⇔(x + 1) (x + 1)(x2 – x + 1) = 0
⇔ (x + 1)2(x2 – x + 1) = 0
⇔ x + 1 = 0 (vì x2 – x + 1 > 0 với mọi x)
⇔ x = -1
Vậy phương trình đã cho có một nghiệm x = -1.
Bài 10: Giải các phương trình sau:
a, (x2 + x)2 + 4(x2 + x) = 0
b, (x – 1)(x – 3)(x + 5)(x + 7) = 0
Hướng dẫn giải:
a, (x2 + x)2 + 4(x2 + x) = 0
⇔ (x2 + x)(x2 + x + 4) = 0
⇔ x(x + 1)(x2 + x + 4) = 0
⇔ x = 0 hoặc x + 1 = 0 (vì x2 + x + 4 > 0 với mọi x)
⇔ x = 0 hoặc x = -1
Vậy phương trình đã cho có hai nghiệm x = 0, x = -1.
b, (x – 1)(x – 3)(x + 5)(x + 7) = 0
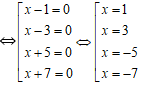
Vậy tập nghiệm của phương trình là S = { -7;-5;1;3}

