Cách vẽ hình đối xứng của một hình cho trước bằng đối xứng trục

Cách vẽ hình đối xứng của một hình cho trước bằng đối xứng trục

Tài liệu Cách vẽ hình đối xứng của một hình cho trước bằng đối xứng trục Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải

Sử dụng định nghĩa của phép đối xứng trục.

a) Hai điểm gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó.

Quy ước: Nếu B∈d thì ta nói B đối xứng với B qua d.

b) Hai hình gọi là đối xứng với nhau qua đường thẳng d nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng d và ngược lại. Đường thẳng d gọi là trục đối xứng của hai hình đó.

Sử dụng tính chất:

Nếu các điểm A và A', B và B' , C và C' đối xứng với nhau qua đường thẳng d trong đó C nằm giữa A và B thì C' nằm giữa A' và B' .

B. Ví dụ minh họa

Ví dụ 1. Cho ΔABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm D. Vẽ điểm E đối xứng với D qua AH.

Giải

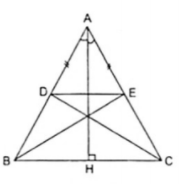
Vì ABC cân tại A có AH là đường cao theo giả thiết nên AH là tia phân giác của góc A.

Vẽ điểm E thuộc cạnh AC sao cho AD = AE nên ∆ADE cân tại A. Suy ra AH là đường trung trực của DE. Vậy D đối xứng với E qua AH.

Ví dụ 2. Cho ΔABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm D, vẽ ΔADC đối xứng với ΔAEB qua AH.

Giải

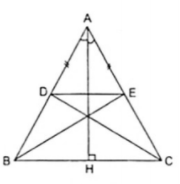
Vì AH là đường cao của ΔABC cân tại A nên AH là đường trung trực của BC suy ra B đối xứng với C qua AH.

Vẽ điểm E thuộc cạnh AC sao cho AD = AE nên ΔADE cân tại A. Suy ra AH là đường trung trực của DE. Vậy D đối xứng với E qua AH.

Lại có A đối xứng với A qua AH theo quy ước. Vậy ΔADC đối xứng với ΔAEB qua AH.

Ví dụ 3. Cho tam giác ABC, trong đó AB = 11 cm, AC = 15 cm. Vẽ hình đối xứng với tam giác ABC qua trục là cạnh BC.

Giải

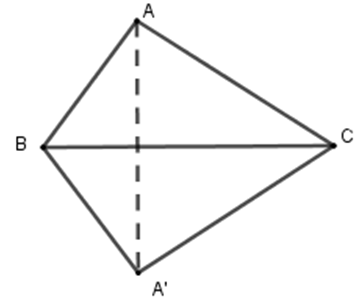
Ta có B đối xứng với B qua BC theo quy ước, C đối xứng với C qua BC theo quy ước

Vẽ đường thẳng d đi qua A và vuông góc với BC. Trên đường thẳng d vẽ điểm A’ sao cho AB = A'B . Suy ra A' là điểm đối xứng với A qua BC. Khi đó tam giác A'BC đối xứng với tam giác ABC qua BC.

Ví dụ 4. Cho hai điểm A, B nằm cùng phía đối với đường thẳng d. Vẽ hai điểm C đối xứng với A qua d và D đối xứng với B qua d.

Giải

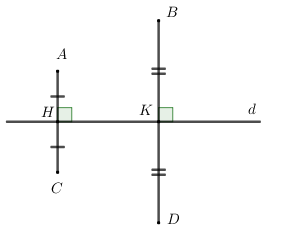
Vẽ 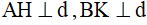. Vẽ hai điểm C, D sao cho H là trung điểm của AC, K là trung điểm của BD ta được C đối xứng với A qua đường thẳng d, D đối xứng với B qua đường thẳng d.

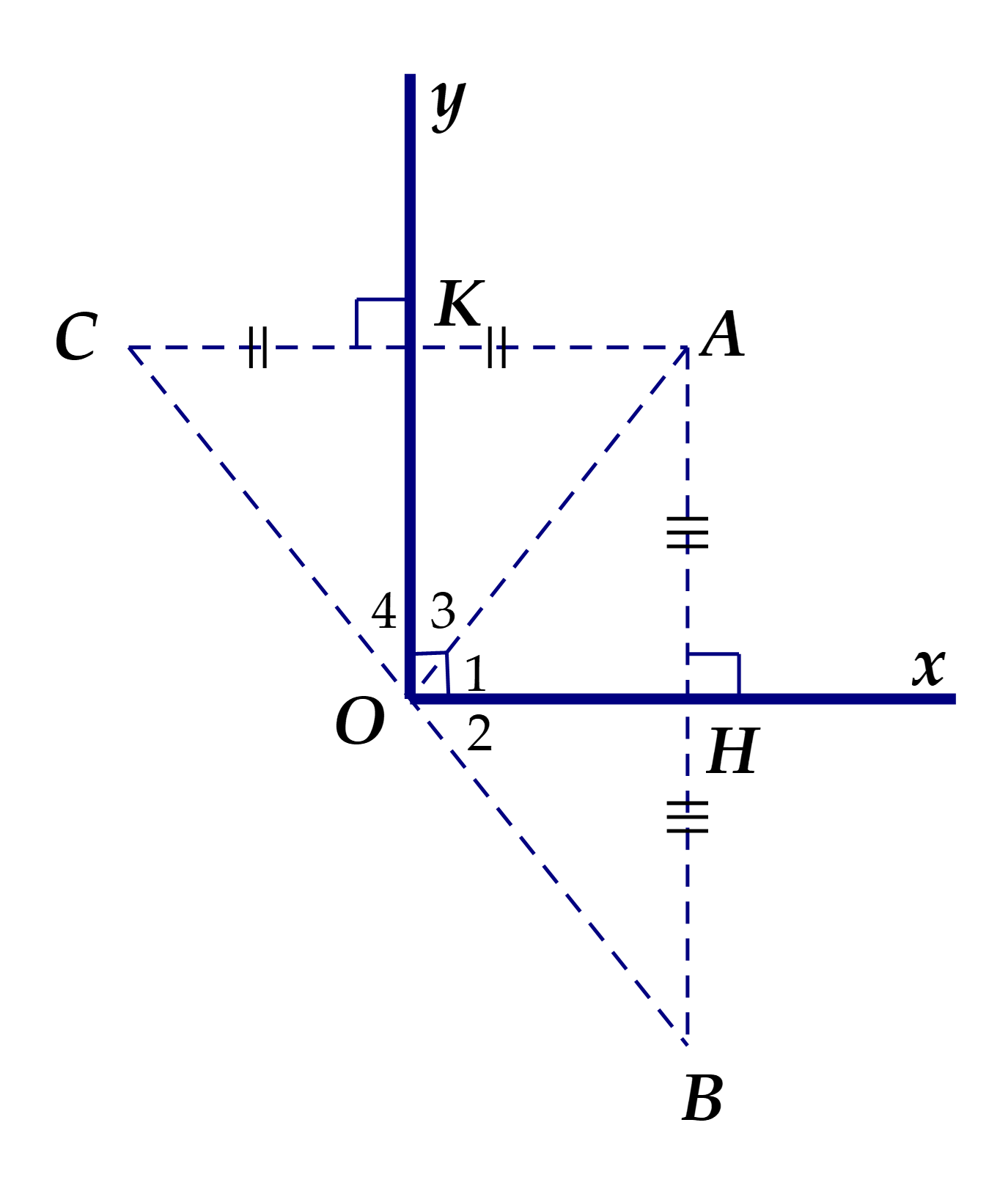
Ví dụ 5. Cho góc vuông xOy, điểm A nằm trong góc đó. Gọi B là điểm đối xứng với A qua Ox, C là điểm đối xứng với A qua Oy. Nêu cách vẽ B và C.

Giải

Vẽ 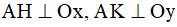, vẽ hai điểm B, C sao cho H, K lần lượt là trung điểm của AB, AC thì B đối xứng với A qua Ox, C đối xứng với A qua Oy.

Vì 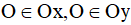đối xứng với O qua Ox, Oy.